Buckling Analysis of Stepped Columns Based on the Improved Fourier Series Method
-
摘要:
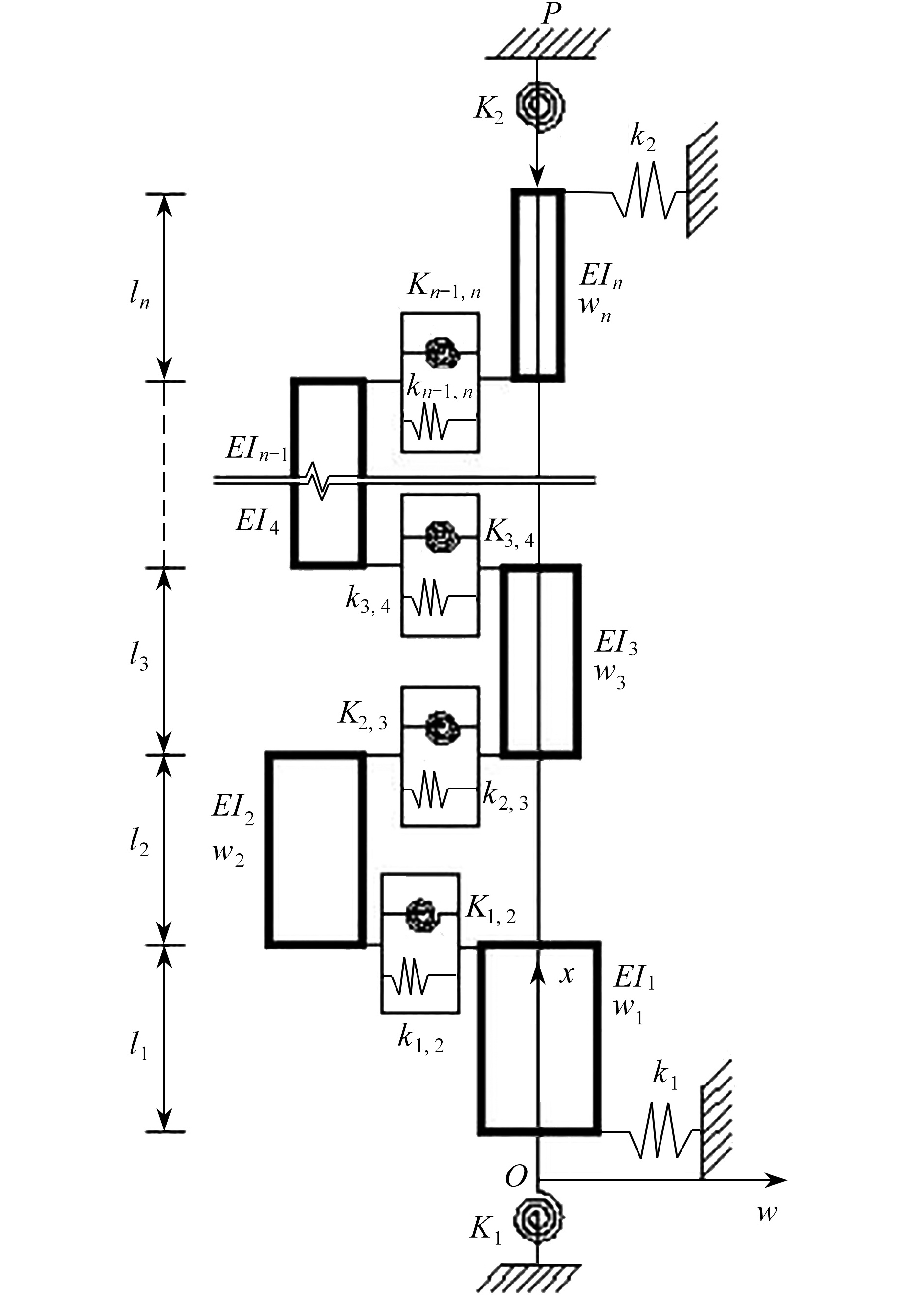
该文对阶梯柱的弹性屈曲问题进行了研究。首先基于改进Fourier级数法采用局部坐标逐段建立阶梯柱的位移函数表达式，然后由带约束的势能变分原理得到含屈曲荷载的线性方程组，利用线性方程组有非零解的条件把问题转化为矩阵特征值问题得到临界载荷，最后讨论方法中的参数取值，并把结果与已有文献和有限元的结果比较，从而验证方法的精度。所提模型在阶梯柱的两端和变截面处引入横向弹簧和旋转弹簧，通过改变弹簧的刚度值模拟不同的边界。所提方法在工程设计中能比较精确地确定各种弹性边界条件下阶梯柱的临界载荷。
-
关键词:
- 改进Fourier级数法 /
- 临界荷载 /
- 带约束的势能变分原理 /
- 阶梯柱
Abstract:The elastic buckling of stepped columns with variable cross sections was studied. Firstly, based on the improved Fourier series method, the displacement function of the column was established in the local coordinate system, then the linear equations for buckling loads were obtained with the constrained variational principle of potential energy. The problem was transformed into a matrix eigenvalue problem and the buckling load was obtained from solution of the matrix eigenvalues. Finally, the parameter values in the method were discussed through numerical examples, and the obtained results were compared with the finite element results and previous literature results so as to verify the accuracy of the method. In the presented model the translational and rotational springs were arranged at the 2 ends and the setback cross sections. The method can determine the buckling loads of stepped columns with various elastic boundary conditions accurately in engineering design.
-
图 2 一端弹性一端自由阶梯柱的临界载荷随刚度参数对数的变化图
Figure 2. Change of buckling loads of the elastic-free stepped column with non-dimensional spring stiffness on a logarithmic scale
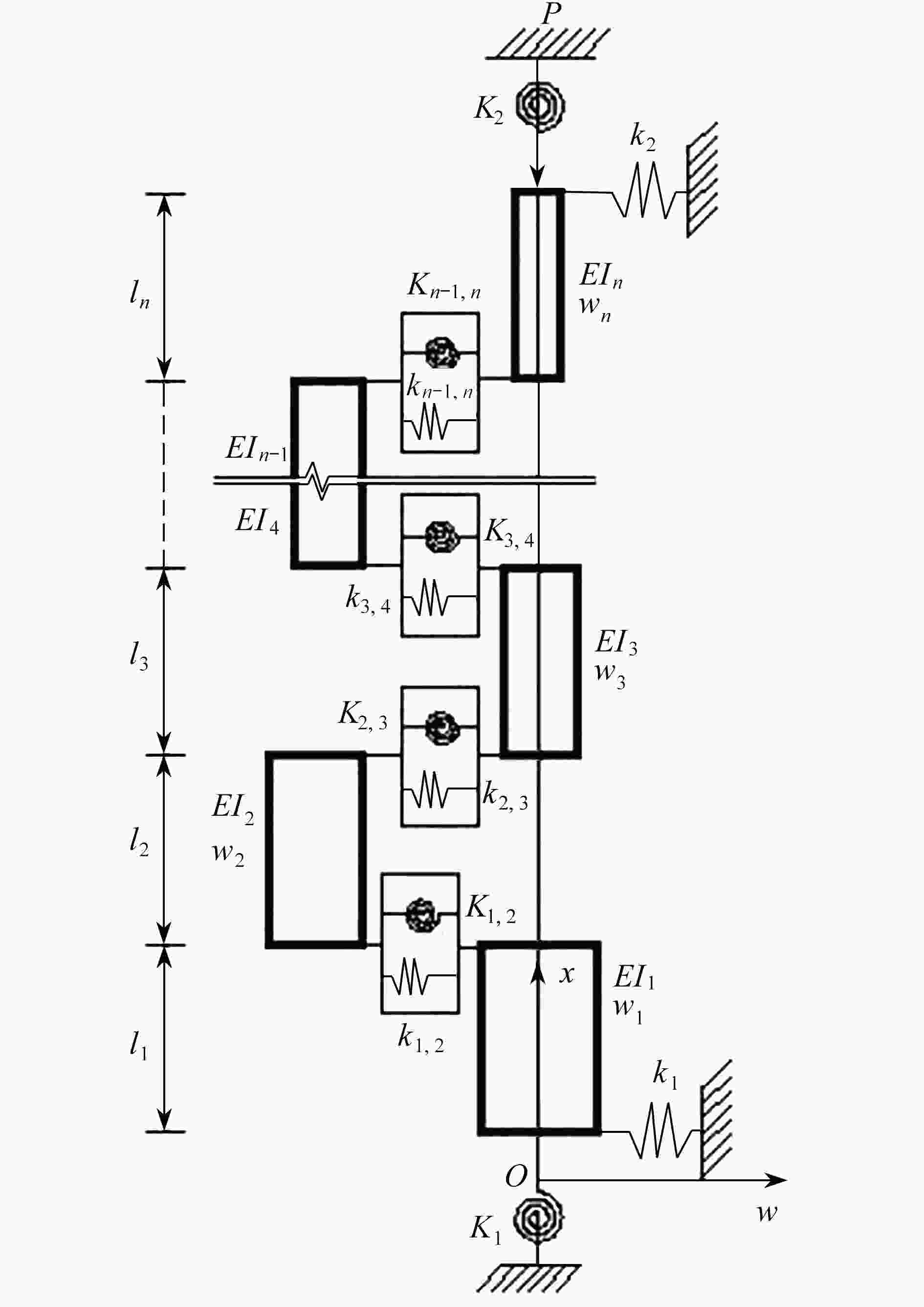
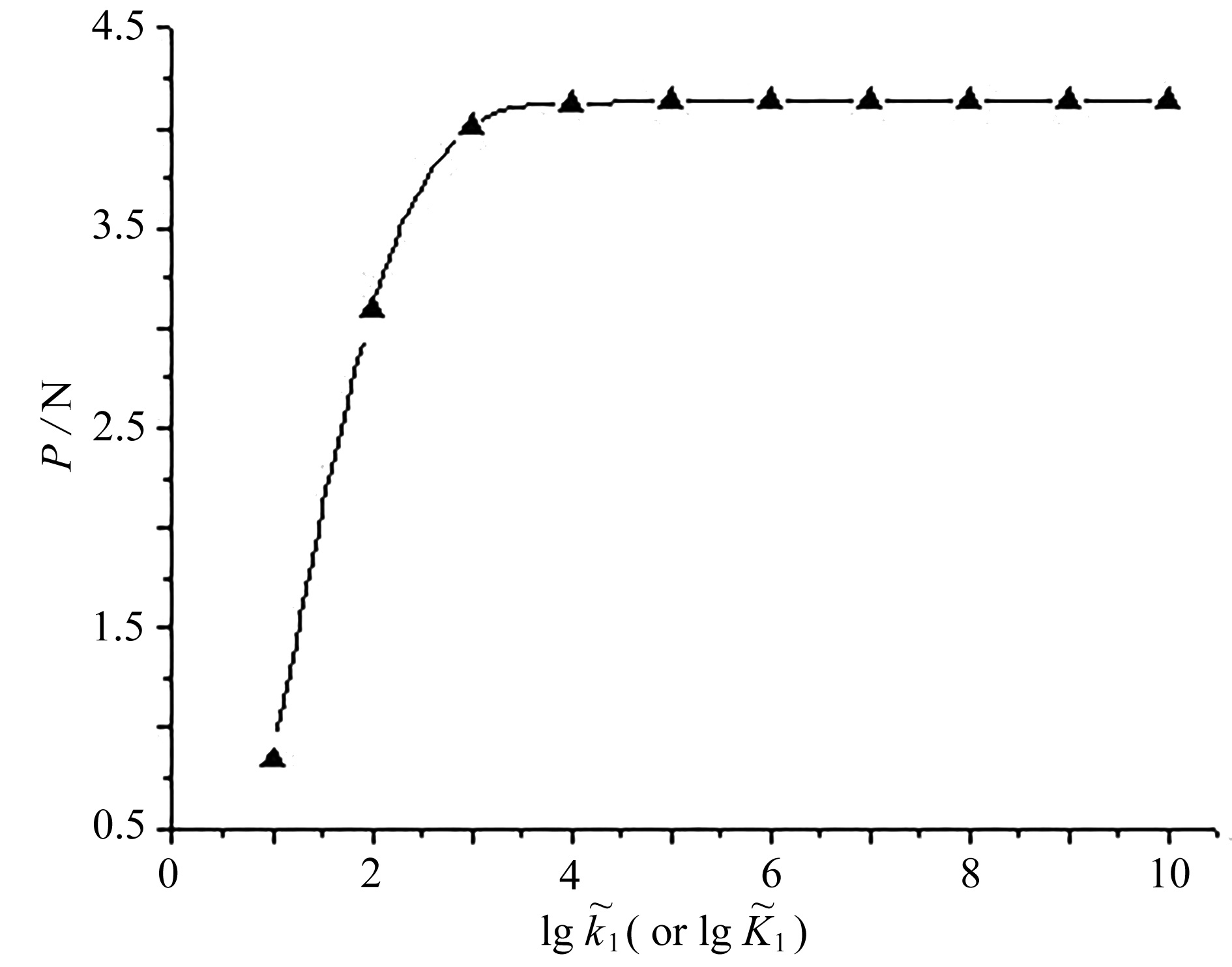
表 1 一端弹性一端自由阶梯柱的屈曲荷载随不同弹簧刚度值的收敛情况
Table 1. Convergence of buckling loads of the elastic-free stepped column with different spring stiffness values
$ {\tilde k_1} = {\tilde K_1} $ 10 102 103 104 105 106 107 108 109 1010 P/N 0.8364 3.0870 4.0082 4.1216 4.1332 4.1344 4.1345 4.1345 4.1345 4.1345 
下载: 导出CSV
表 2 一端固定一端自由阶梯柱的屈曲荷载随M的收敛情况
Table 2. Convergence of buckling loads of the clamped-free stepped column with different M values
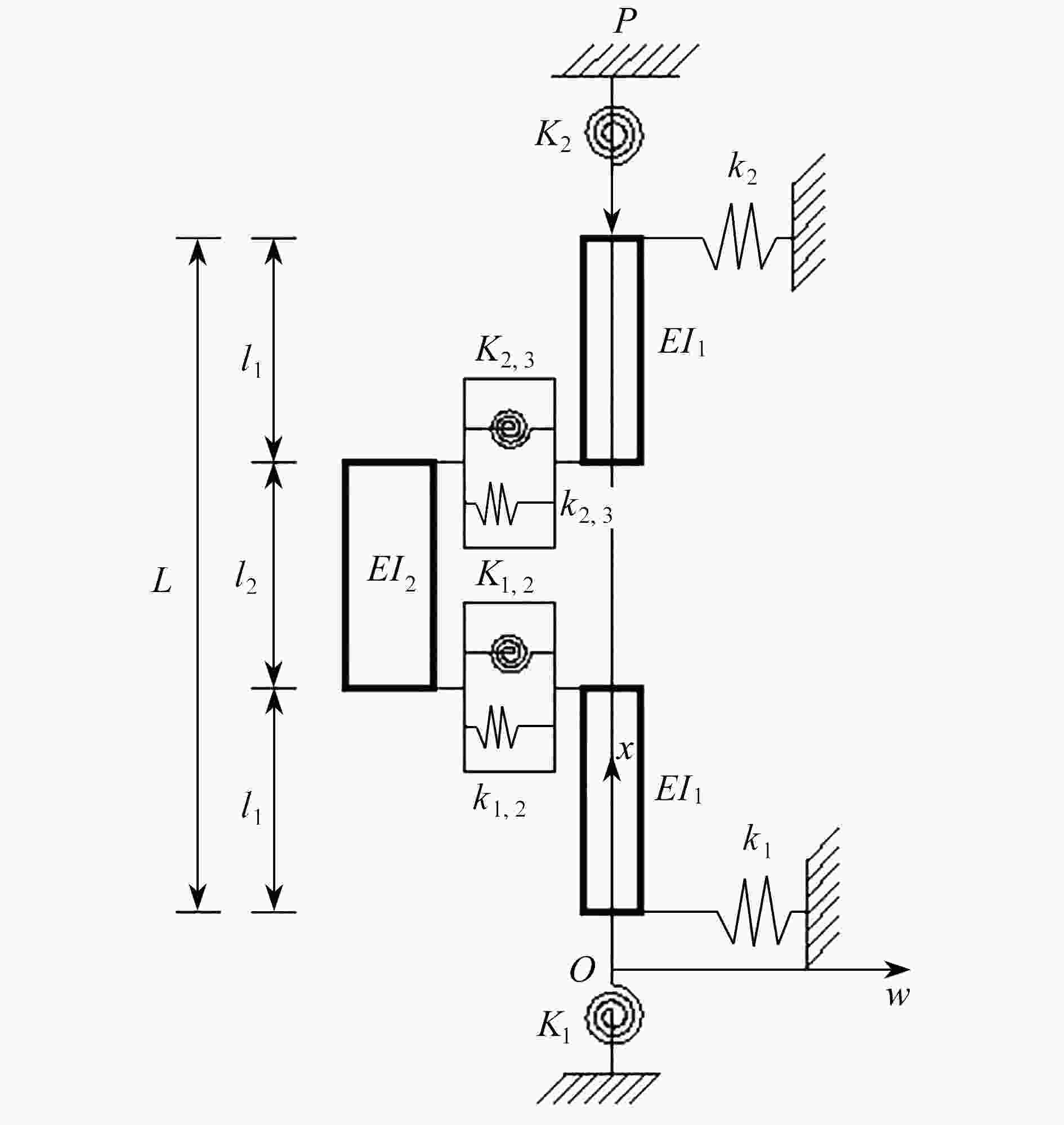
M 4 6 8 10 12 14 16 18 20 P/N 4.2213 4.1393 4.1351 4.1346 4.1345 4.1345 4.1345 4.1345 4.1345
下载: 导出CSV
表 3 一端固定一端自由阶梯柱的计算长度系数及误差
Table 3. The effective length coefficients and errors of clamped-free stepped columns
μ2 I1/I2 l1/L 0.2 0.3 0.4 0.5 0.6 0.7 0.8 this paper 2.5 1.404 1.302 1.216 1.139 1.077 1.034 1.010 ref. [5] 1.39 1.30 1.22 1.14 1.08 1.03 1.01 error δ/% 1.007 0.154 0.328 0.088 0.278 0.389 0.000 this paper 2 1.274 1.208 1.146 1.093 1.051 1.022 1.007 ref. [5] 1.27 1.21 1.14 1.09 1.05 1.02 1.01 error δ/% 0.315 0.165 0.526 0.275 0.095 0.196 0.297 this paper 1.75 1.211 1.158 1.110 1.069 1.038 1.021 1.006 ref. [5] 1.21 1.16 1.11 1.07 1.04 1.02 1.00 error δ/% 0.083 0.172 0 0.093 0.192 0.098 0.6 this paper 1.5 1.144 1.107 1.074 1.050 1.025 1.011 1.003 ref. [5] 1.14 1.11 1.07 1.05 1.02 1.01 1.00 error δ/% 0.351 0.270 0.374 0.000 0.490 0.099 0.3 this paper 1 1.000 1.000 1.000 1.000 1.000 1.000 1.000 ref. [5] 1.00 1.00 1.00 1.00 1.00 1.00 1.00 error δ/% 0.000 0.000 0.000 0.000 0.000 0.000 0.000
下载: 导出CSV
表 4 一端固定一端弹性阶梯柱的屈曲载荷值(单位: N)
Table 4. The buckling loads of the clamped-free stepped column (unit: N)
I1/I2 l1/L $ {\tilde K_2} = {\tilde k_2} $ 0 10 103 105 107 108 2.5 0.3 4.1119 5.5297 10.5149 10.6476 10.6489 10.6489 0.5 3.8030 24.2575 43.1497 44.0280 44.3069 44.0370 2 0.3 5.1399 6.5968 13.1087 13.3091 13.3111 13.3111 0.5 4.1345 27.6652 50.3485 51.6053 51.6181 51.6183 1.75 0.3 5.8742 7.3510 14.9482 15.2101 15.2127 15.2127 0.5 4.3168 29.9558 55.0281 56.5625 56.5782 56.5783 1.5 0.3 6.8532 8.3501 17.3881 17.7446 17.7481 17.7481 0.5 4.5108 32.8297 60.6880 62.5874 62.6069 62.6071 1.0 0.3 10.2799 11.8173 25.8119 26.6141 26.6221 26.6222 0.5 4.9349 41.3393 75.9055 78.9252 78.9565 78.9567
下载: 导出CSV
表 5 两端铰支阶梯柱的屈曲系数及误差
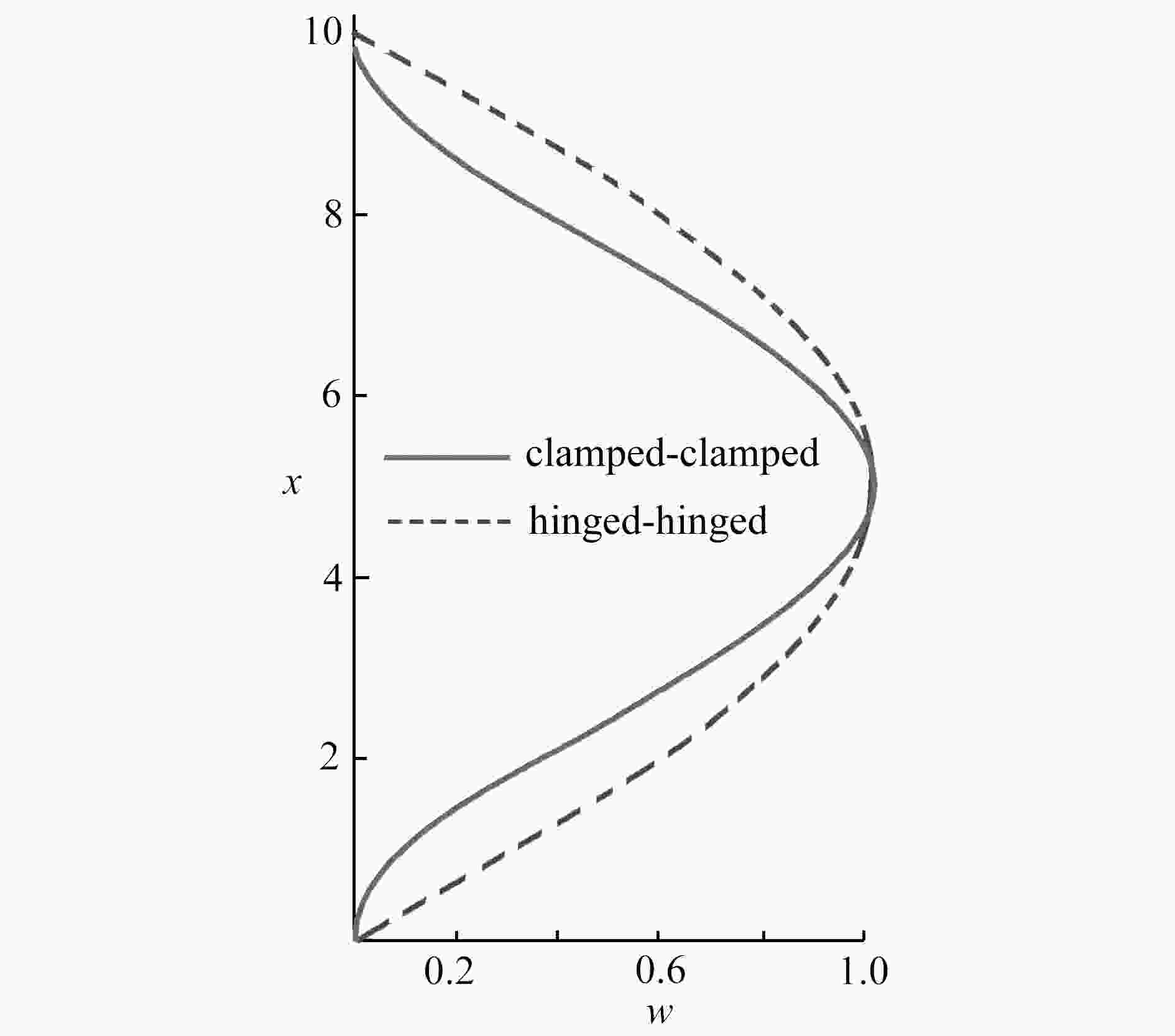
Table 5. Buckling factors and errors of stepped columns with hinged ends
I1/I2 l2/L 0.2 0.3 0.4 0.5 0.6 0.7 0.8 FEM 0.2 2.7955 3.4062 4.2218 5.3094 6.6942 8.1970 9.3302 this paper 2.7955 3.4062 4.2218 5.3094 6.6942 8.1971 9.3303 error δ/% 0.0000 0.0000 0.0000 0.0000 0.0000 0.0012 0.0011 FEM
0.45.0885 5.8256 6.6774 7.6060 8.5098 9.2360 9.6742 this paper 5.0884 5.8256 6.6774 7.6060 8.5099 9.2361 9.6744 error δ/% 0.0020 0.0000 0.0000 0.0000 0.0012 0.0011 0.0021 FEM 0.6 6.9794 7.5759 8.1850 8.7602 9.2438 9.5888 9.7839 this paper 6.9794 7.5759 8.1851 8.7603 9.2439 9.5890 9.7841 error δ/% 0.0000 0.0000 0.0012 0.0011 0.0011 0.0021 0.0020 FEM 0.8 8.5512 8.8764 9.1767 9.4334 9.6315 9.7646 9.8377 this paper 8.5513 8.8764 9.1768 9.4335 9.6316 9.7648 9.8380 error δ/% 0.0012 0.0000 0.0011 0.0011 0.0010 0.0020 0.0030
下载: 导出CSV
表 6 两端固定阶梯柱的屈曲系数及误差
Table 6. Buckling factors and errors of stepped columns with clamped ends
I1/I2 l2/L 0.2 0.3 0.4 0.5 0.6 0.7 0.8 FEM 0.2 11.1574 13.4813 16.2613 18.9643 20.4594 20.6714 21.0548 this paper 11.1574 13.4813 16.2613 18.9643 20.4594 20.6714 21.0548 error δ/% 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 FEM
0.420.2377 22.7428 24.8856 26.0625 26.3025 26.4150 27.4675 this paper 20.2377 22.7428 24.8856 26.0627 26.3013 26.4170 27.4671 error δ/% 0.0000 0.0000 0.0000 0.0008 0.0046 0.0076 0.0015 FEM 0.6 27.7150 29.4950 30.6450 31.0550 31.0875 31.3475 32.4550 this paper 27.7154 29.4960 30.6447 31.0541 31.0865 31.3493 32.4559 error δ/% 0.0014 0.0034 0.0010 0.0029 0.0032 0.0057 0.0028 FEM 0.8 34.0200 34.8750 35.3150 35.4200 35.4400 35.6755 36.3725 this paper 34.0194 34.8758 35.3153 35.4195 35.4401 35.6754 36.3713 error δ/% 0.0018 0.0023 0.0010 0.0014 0.0003 0.0003 0.0033
下载: 导出CSV
-
[1] TIMOSHENKO S P, GERE J M. Theory of Elastic Stability[M]. New York: McGraw-Hill, 1961: 49-63. [2] 都亮, 陆念力, 兰朋. 弹性支撑阶梯柱侧向位移与稳定性的精确分析[J]. 哈尔滨工程大学学报, 2014, 8(35): 993-996. (DU Liang, LU Nianli, LAN Peng. Accurate analysis of lateral displacement and stability of stepped columns with elastic supports[J]. Journal of Harbin University of Engineering, 2014, 8(35): 993-996.(in Chinese) [3] LI Q S. Buckling analysis of multi-step non-uniform columns[J]. Advances in Structural Engineering, 2000, 3(2): 139-144. doi: 10.1260/1369433001502085 [4] PARK J S, STALLINGS J M. Lateral-torsional buckling of stepped beams with continuous bracing[J]. Journal of Bridge Engineering, 2005, 10(1): 87-95. doi: 10.1061/(ASCE)1084-0702(2005)10:1(87) [5] 陆念力, 都亮, 兰朋. 变截面阶梯压杆精确失稳特征方程及其稳定计算实用方法[J]. 建筑机械, 2014(3): 76-81. (LU Nianli, DU Liang, LAN Peng. Accurate buckling characteristic equation of stepped column bar and its stability analysis with practical method: shortcut calculation and accuracy analysis with the effective length of stepped column given in specification for tower crane design[J]. Construction Machinery, 2014(3): 76-81.(in Chinese) [6] 姚峰林, 孟文俊, 赵婕, 等. 起重机n阶伸缩臂架稳定性的递推公式及数值解法[J]. 中国机械工程, 2019, 30(21): 2533-2538. (YAO Fenglin, MENG Wenjun, ZHAO Jie, et al. Recurrence formula and numerical solution of n-stage telescopic boom stability of crane[J]. China Mechanical Engineering, 2019, 30(21): 2533-2538.(in Chinese) doi: 10.3969/j.issn.1004-132X.2019.21.003 [7] 谢海, 寿开荣, 李龙, 等. 基于最小势能原理的变截面压杆临界压力的计算方法[J]. 浙江理工大学学报, 2013, 30(1): 87-89. (XIE Hai, SHOU Kairong, LI Long, et al. Calculation method of critical pressure of variable cross section compression bar based on the principle of minimum potential energy[J]. Journal of Zhejiang Sci-Tech University, 2013, 30(1): 87-89.(in Chinese) [8] 刘士明, 陆念力, 寇捷. 起重机箱形伸缩臂整体稳定性分析[J]. 中国工程机械学报, 2010, 8(1): 29-34. (LIU Shiming, LU Nianli, KOU Jie. Global stability analysis on crane telescopic boom[J]. Chinese Journal of Constrution Machinery, 2010, 8(1): 29-34.(in Chinese) doi: 10.3969/j.issn.1672-5581.2010.01.006 [9] 王俊飞, 姚峰林, 佘占蛟. 截面尺寸对伸缩臂屈曲失稳性能的影响[J]. 中国工程机械学报, 2018, 16(4): 305-315. (WANG Junfei, YAO Fenglin, SHE Zhanjiao. Influence of section size on buckling and instability performance of telescopic boom[J]. Chinese Journal of Engineering Machinery, 2018, 16(4): 305-315.(in Chinese) [10] 姚峰林, 孟文俊, 赵婕, 等. 伸缩臂式起重机阶梯柱模型的临界力计算对比[J]. 机械设计与制造, 2020, 5(5): 23-27. (YAO Fenglin, MENG Wenjun, ZHAO Jie, et al. Calculation comparison of critical force of ladder column model of telescopic crane[J]. Mechanical Design and Manufacturing, 2020, 5(5): 23-27.(in Chinese) doi: 10.3969/j.issn.1001-3997.2020.05.006 [11] 龚相超, 钟冬望, 杨泰华, 等. 基于阶梯压杆模型和最小势能原理的立柱爆高计算[J]. 爆破, 2012, 29(3): 27-30, 41. (GONG Xiangchao, ZHONG Dongwang, YANG Taihua, et al. Calculation of column explosion height based on stepped strut model and minimum potential energy principle[J]. Blasting, 2012, 29(3): 27-30, 41.(in Chinese) doi: 10.3963/j.issn.1001-487X.2012.03.007 [12] 王欣, 易怀军, 赵日鑫, 等. 一种n阶变截面压杆稳定性计算方法的研究[J]. 中国机械工程, 2014, 25(13): 1744-1747, 1799. (WANG Xin, YI Huaijun, ZHAO Rixin, et al. Research on stability analysis method of n-order variable cross-section compression bars[J]. China Mechanical Engineering, 2014, 25(13): 1744-1747, 1799.(in Chinese) doi: 10.3969/j.issn.1004-132X.2014.13.009 [13] LI W L. Free vibrations of beams with general boundary conditions[J]. Journal of Sound and Vibration, 2000, 237(4): 709-725. doi: 10.1006/jsvi.2000.3150 [14] LI W L. Vibration anaiysis of rectangular plates with general elastic boundary supports[J]. Journal of Sound and Vibration, 2004, 273(3): 619-635. doi: 10.1016/S0022-460X(03)00562-5 [15] 肖伟, 霍瑞东, 李海超, 等. 改进傅里叶方法在梁结构振动特性分析中的应用[J]. 噪声与振动控制, 2019, 39(1): 10-15. (XIAO Wei, HUO Ruidong, LI Haichao, et al. Application of improved Fourier method in vibration characteristics analysis of beam structures[J]. Noise and Vibration Control, 2019, 39(1): 10-15.(in Chinese) doi: 10.3969/j.issn.1006-1355.2019.01.003 [16] 鲍四元, 曹津瑞, 周静. 任意弹性边界下非局部梁的横向振动特性研究[J]. 振动工程学报, 2020, 33(4): 276-284. (BAO Siyuan, CAO Jinrui, ZHOU Jing. Transverse vibration characteristics of nonlocal beams with arbitrary boundary conditions[J]. Journal of Vibration Engineering, 2020, 33(4): 276-284.(in Chinese) [17] 鲍四元, 周静, 陆健炜. 任意弹性边界的多段梁自由振动研究[J]. 应用数学和力学, 2020, 41(9): 985-993. (BAO Siyuan, ZHOU Jing, LU Jianwei. Free vibrations of multi-segment beams with arbitrary boundary conditions[J]. Applied Mathematics and Mechanics, 2020, 41(9): 985-993.(in Chinese) -
计量
- 文章访问数: 896
- HTML全文浏览量: 351
- PDF下载量: 56
- 被引次数: 0
渝公网安备50010802005915号