二维瞬态热传导的PDDO分析

周保良; 李志远; 黄丹

doi:10.21656/1000-0887.420150

二维瞬态热传导的PDDO分析

doi: 10.21656/1000-0887.420150

河海大学力学与材料学院，南京 211100

基金项目: 国家自然科学基金（12072104；51679077；11932006）；国家重点研发计划（2018YFC0406703）

详细信息

作者简介:
周保良（1998—），男，硕士（E-mail：zhoubaoliang2020@126.com）

黄丹（1979—），男，教授（通讯作者. E-mail：danhuang@hhu.edu.cn）

中图分类号: O302
计量
- 文章访问数: 1230
- HTML全文浏览量: 516
- PDF下载量: 99
- 被引次数: 0
出版历程
- 收稿日期: 2021-06-02
- 修回日期: 2021-10-07
- 网络出版日期: 2022-05-30
- 刊出日期: 2022-06-30

PDDO Analysis of 2D Transient Heat Conduction Problems

College of Mechanics and Materials, Hohai University, Nanjing 211100, P.R.China

摘要

摘要:
采用近场动力学微分算子(peridynamic differential operator, PDDO)理论求解了二维瞬态热传导问题。将热传导方程和边界条件由其局部微分形式重构为非局部积分形式，引入Lagrange乘数法，采用变分原理的概念，建立了二维瞬态热传导问题的非局部分析模型。通过误差与收敛性分析，与其他数值方法计算结果进行比较，验证了本模型的准确性。在此基础上，将本模型应用于计算不规则边界板和内部含微缺陷(裂纹和圆孔)板的二维瞬态热传导问题。结果表明该方法计算精度高、适用范围广、具有较好的收敛性，为计算二维瞬态热传导问题提供了新的思路。
- 近场动力学微分算子 /
- 二维瞬态热传导 /
- 不规则边界板 /
- 含微缺陷板
Abstract:
The peridynamic differential operator (PDDO) theory was introduced to solve the 2D transient heat conduction problems. The heat conduction equation and the boundary condition were reformulated from the local differential form to the non-local integral form. Then the Lagrangian multiplier method and the variational analysis were used, and a non-local model for 2D transient heat conduction problems was established. Through error and convergence analysis, the accuracy of this model was verified in comparison with the results of other numerical methods. The model was further applied to solve the 2D transient heat conduction problems of plates with irregular boundaries and micro-defects (cracks and holes). The results show high accuracy, wide applicability and good convergence of this method, which provides new insights into the 2D transient heat conduction problems.
- peridynamic differential operator /
- 2D transient heat conduction /
- irregular-boundary plate /
- micro-defect plate

HTML全文

图 1 物质点在任意形状近场范围内的相互作用

Figure 1. Interaction of material points within an arbitrary-shape near field

下载: 全尺寸图片幻灯片

图 2 方形板及边界条件

Figure 2. A square plate and its boundary conditions

下载: 全尺寸图片幻灯片

图 3 瞬态温度场的PDDO误差测量值

Figure 3. The error measure of the PDDO solution for the transient temperature field

下载: 全尺寸图片幻灯片

图 4 A、B、C板的几何形状和边界条件

Figure 4. Geometric shapes and boundary conditions of plates A, B and C

下载: 全尺寸图片幻灯片

图 5 t=0.8 s时，A、B、C三种形状的板在不同方法下沿指定路径的温度分布

Figure 5. Temperature distributions of plates A, B and C along a specified path for different methods at t=0.8 s

下载: 全尺寸图片幻灯片

图 6 稳态时，A板在不同数值方法下的温度分布：（a） FEM^[21]；（b） RBF-DQ^[21]；（c） PDDO

Figure 6. Temperature distributions of plate A for different numerical methods in a steady state: （a） FEM^[21]; （b） RBF-DQ^[21]; （c） PDDO

下载: 全尺寸图片幻灯片

图 7 稳态时，B板在不同数值方法下的温度分布：（a） FEM^[21]；（b） RBF-DQ^[21]；（c） PDDO

注　为了解释图中的颜色，读者可以参考本文的电子网页版本，后同。

Figure 7. Temperature distributions of plate B for different numerical methods in a steady state: （a） FEM^[21]; （b） RBF-DQ^[21]; （c） PDDO

下载: 全尺寸图片幻灯片

图 8 稳态时，C板在不同数值方法下的温度分布：（a） FEM^[21]；（b） RBF-DQ^[21]；（c） PDDO

Figure 8. Temperature distributions of plate C for different numerical methods in a steady state: （a） FEM^[21]; （b） RBF-DQ^[21]; （c） PDDO

下载: 全尺寸图片幻灯片

图 9 含裂纹板和含圆孔板模型

Figure 9. The models for plates containing a crack or a hole

下载: 全尺寸图片幻灯片

图 10 稳态时，含裂纹板在不同数值方法下的温度分布：（a） FEM；（b） PDDO

Figure 10. Temperature distributions of plates containing cracks for different numerical methods in steady states: （a） FEM; （b） PDDO

下载: 全尺寸图片幻灯片

图 11 稳态时，含圆孔板在不同数值方法下的温度分布：（a） FEM；（b） PDDO

Figure 11. Temperature distributions of plates containing holes for different numerical methods in steady states: （a） FEM; （b） PDDO

下载: 全尺寸图片幻灯片

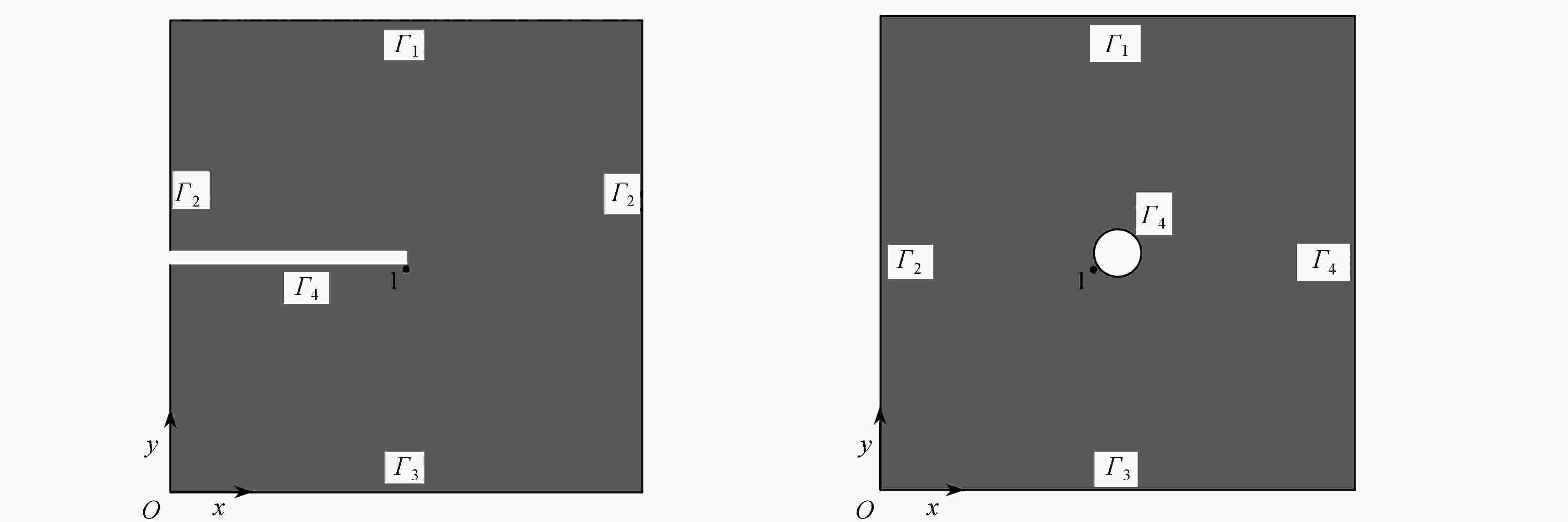
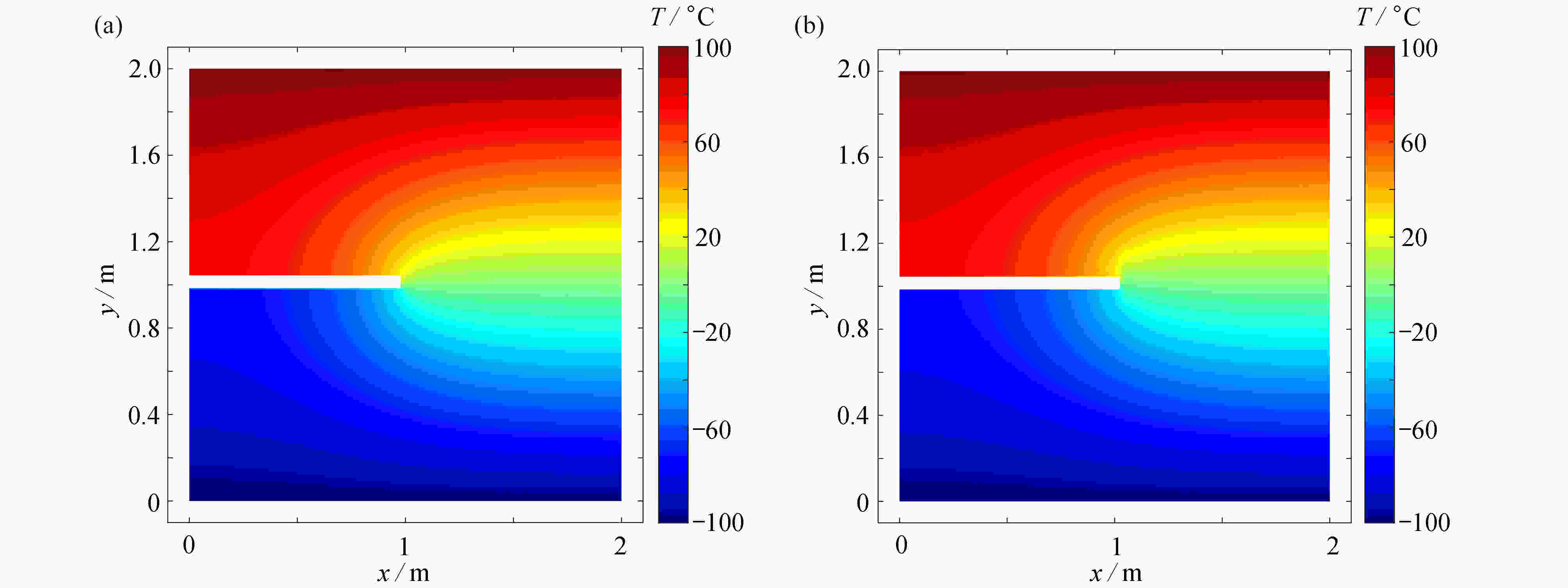
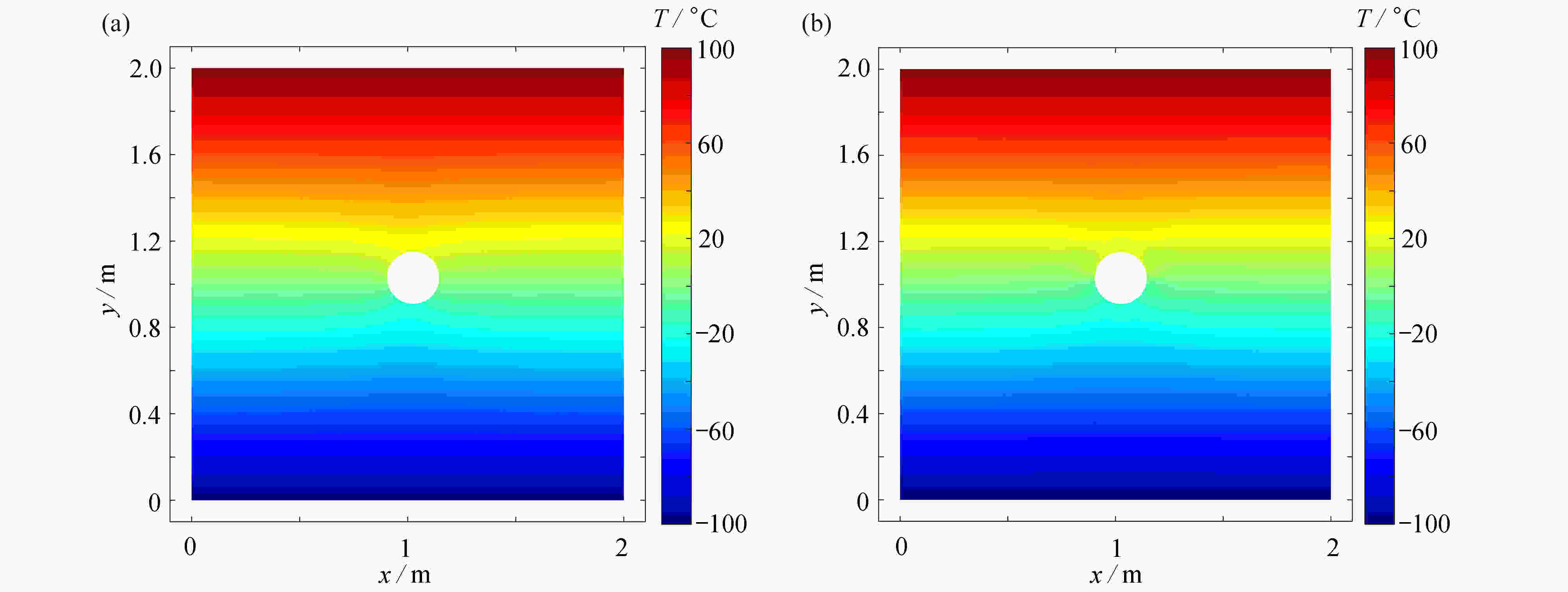
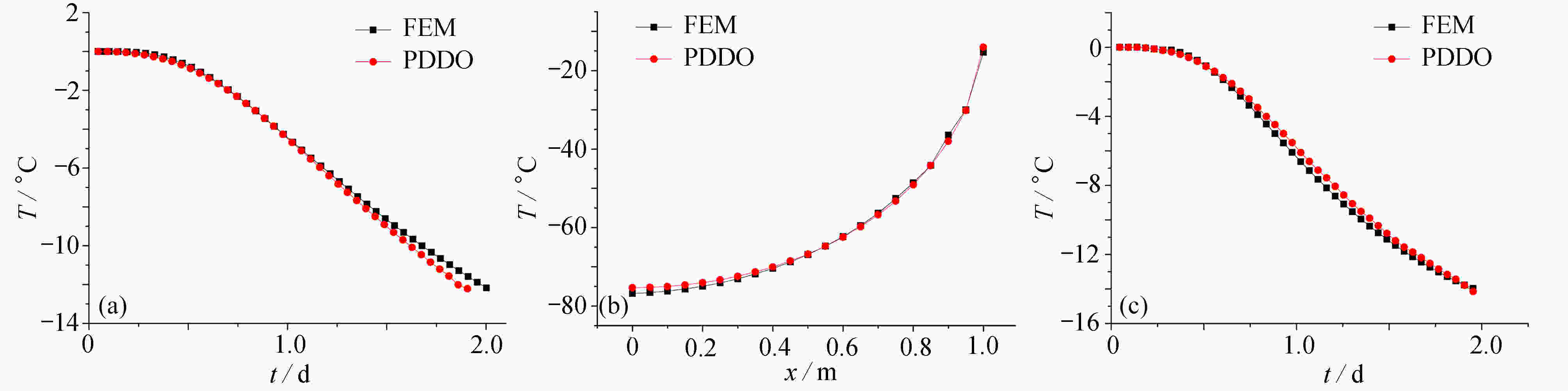
图 12 含裂纹板和含圆孔板在不同数值方法下的温度变化曲线：（a）含裂纹板测点处，温度随时间的变化曲线；（b）稳态时，温度沿裂纹的下边界变化的曲线；（c）含圆孔板测点处，温度随时间的变化曲线

Figure 12. The temperature variation curves of plates containing a crack or a hole for different numerical methods: （a） temperature change curves with time at the measuring point of the plate containing a crack; （b）temperature curves along the lower boundary of the crack in a steady state; （c） temperature change curves with time at the measuring point of the plate containing a hole

下载: 全尺寸图片幻灯片

表 1 t=1.2 h时不同方法的数值结果比较

Table 1. Comparison of numerical results between different methods at t =1.2 h

point	(x, y)/m	PDDO	BKM	FEM	BEM	DRBEM	Trefftz FEM	exact solution
a	(2.4,1.5)	1.081	1.081	1.139	1.114	1.099	1.103	1.065
b	(2.4,2.4)	0.637	0.631	0.670	0.657	0.645	0.660	0.626
c	(1.8,1.5)	1.745	1.779	1.843	1.798	1.784	1.797	1.723
d	(1.8,1.8)	1.660	1.691	1.753	1.713	1.695	1.715	1.639
e	(1.5,1.5)	1.834	1.871	1.938	1.887	1.877	1.894	1.812

下载: 导出CSV

参考文献(21)

[1]	王红, 李小林. 二维瞬态热传导问题的无单元Galerkin法分析[J]. 应用数学和力学, 2021, 42(5): 460-469. (WANG Hong, LI Xiaolin. Analysis of 2D transient heat conduction problems with the element-free Galerkin method[J]. Applied Mathematics and Mechanics, 2021, 42(5): 460-469.(in Chinese) WANG Hong, LI Xiaolin. Analysis of 2D transient heat conduction problems with the element-free Galerkin method[J]. Applied Mathematics and Mechanics, 2021, 42(5): 460-469. (in Chinese))
[2]	ZIENIUK E, SAWICKI D. Modification of the classical boundary integral equation for two dimensional transient heat conduction with internal heat source, with the use of NURBS for boundary modeling[J]. Journal of Heat Transfer, 2017, 139(8): 81-95.
[3]	BURLAYENKO V N, ALTENBACH H, SADOWSKI T, et al. Modelling functionally graded materials in heat transfer and thermal stress analysis by means of graded finite elements[J]. Applied Mathematical Modelling, 2017, 45(5): 422-438.
[4]	WU X H, TAO W Q. Meshless method based on the local weak-forms for steady state heat conduction problems[J]. International Journal of Heat and Mass Transfer, 2008, 51(11/12): 3103-3112.
[5]	BREBBIA C A, TELLES J C F, WROBEL L C. Boundary Element Techniques: Theory and Applications in Engineering[M]. Berlin: Springer Verlag, 1984.
[6]	师晋红, 傅卓佳, 陈文. 边界节点法计算二维瞬态热传导问题[J]. 应用数学和力学, 2014, 35(2): 111-120. (SHI Jinhong, FU Zhuojia, CHEN Wen. Boundary knot method for 2D transient heat conduction problems[J]. Applied Mathematics and Mechanics, 2014, 35(2): 111-120.(in Chinese) doi: 10.3879/j.issn.1000-0887.2014.02.001 SHI Jinhong, FU Zhuojia, CHEN Wen. Boundary knot method for 2D transient heat conduction problems[J]. Applied Mathematics and Mechanics, 2014, 35(2): 111-120. (in Chinese)) doi: 10.3879/j.issn.1000-0887.2014.02.001
[7]	PARTRIDGE P W, BREBBIA C A, WROBEL L C. The Dual Reciprocity Boundary Element Method[M]. Southampton: Computational Mechanics Publications, 1992.
[8]	JIROUSEK J, QIN Q H. Application of hybrid-Trefftz element approach to transient heat conduction analysis[J]. Computers & Structures, 1996, 58(1): 195-201.
[9]	SILLING S A, EPTON M, WECKNER O, et al. Peridynamic states and constitutive modeling[J]. Journal of Elasticity, 2007, 88(2): 151-184. doi: 10.1007/s10659-007-9125-1
[10]	黄丹, 章青, 乔丕忠, 等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40(4): 448-459. (HUANG Dan, ZHANG Qing, QIAO Pizhong, et al. A review on peridynamics(PD)method and its applications[J]. Advances in Mechanics, 2010, 40(4): 448-459.(in Chinese) doi: 10.6052/1000-0992-2010-4-J2010-002 HUANG Dan, ZHANG Qing, QIAO Pizhong, et al. A review on peridynamics(pd)method and its applications[J]. Advances in Mechanics, 2010, 40(4): 448-459. (in Chinese)) doi: 10.6052/1000-0992-2010-4-J2010-002
[11]	MADENCI E, BARYT A, DORDUNCU M. Peridynamic Differential Operator for Numerical Analysis[M]. Switzerland: Springer Nature Switzerland AG, 2019.
[12]	MADENCI E, BARUT A, FUTCH M. Peridynamic differential operator and its applications[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 304: 408-451. doi: 10.1016/j.cma.2016.02.028
[13]	BAZAZZADEH S, SHOJAEI A, ZACCARIOTTO M, et al. Application of the peridynamic differential operator to the solution of sloshing problems in tanks[J]. Engineering Computations, 2018, 36(1): 45-83. doi: 10.1108/EC-12-2017-0520
[14]	DORDUNCU M. Stress analysis of laminated composite beams using refined zigzag theory and peridynamic differential operator[J]. Composite Structures, 2019, 218: 193-203. doi: 10.1016/j.compstruct.2019.03.035
[15]	DORDUNCU M. Stress analysis of sandwich plates with functionally graded cores using peridynamic differential operator and refined zigzag theory[J]. Thin-Walled Structures, 2020, 146: 106468. doi: 10.1016/j.tws.2019.106468
[16]	GAO Y, OTERKUS S. Nonlocal modeling for fluid flow coupled with heat transfer by using peridynamic differential operator[J]. Engineering Analysis With Boundary Elements, 2019, 105: 104-121. doi: 10.1016/j.enganabound.2019.04.007
[17]	GAO Y, OTERKUS S. Nonlocal numerical simulation of low Reynolds number laminar fluid motion by using peridynamic differential operator[J]. Ocean Engineering, 2019, 179: 135-158. doi: 10.1016/j.oceaneng.2019.03.035
[18]	LI Z Y, HUANG D, XU Y P, et al. Nonlocal steady-state thermoelastic analysis of functionally graded materials by using peridynamic differential operator[J]. Applied Mathematical Modelling, 2021, 93: 294-313. doi: 10.1016/j.apm.2020.12.004
[19]	CUI M, XU B B, FENG W Z, et al. A radial integration boundary element method for solving transient heat conduction problems with heat sources and variable thermal conductivity[J]. Numerical Heat Transfer, 2018, 73: 1-18.
[20]	SOLEIMANI S, JALAAL M, BARARNIA H, et al. Local RBF-DQ method for two dimensional transient heat conduction problems[J]. International Communications in Heat and Mass Transfer, 2010, 37(9): 1411-1418. doi: 10.1016/j.icheatmasstransfer.2010.06.033
[21]	MUKHERJEE Y X, MUKHERJEE S. On boundary conditions in the element-free Galerkin method[J]. Computational Mechanics, 1997, 19(4): 264-270. doi: 10.1007/s004660050175