图  1  从2010年1月到2018年12月甘肃省植被覆盖度随年变化的柱状图

Figure  1.  Time series of vegetation coverages in Gansu Province from Jan., 2010 to Dec., 2018

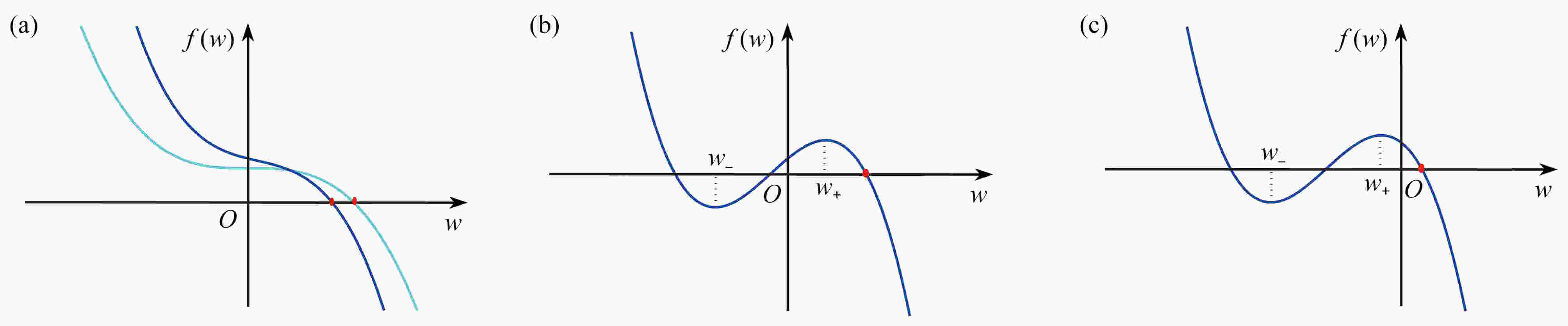
图  2  方程(4)存在唯一正实数根的示意图：(a) 情形(Ⅰ)；(b) 情形(Ⅱ)(i)；(c) 情形(Ⅱ)(ii)(其中红色实心点代表正实数根，图(a)中亮蓝色和蓝色曲线分别表示$\varDelta=0$和$\varDelta < 0$的情形)

注　为了解释图中的颜色，读者可以参考本文的电子网页版本，后同。

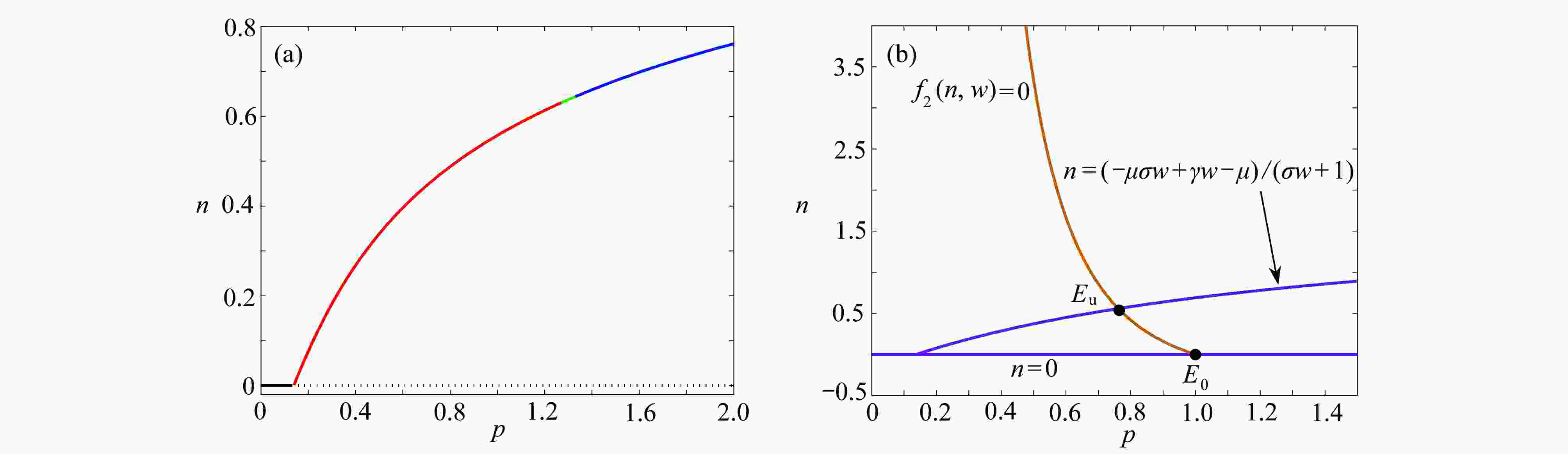
Figure  2.  Schematic diagrams of the existence of the unique positive real root for eq. (4): (a) case (Ⅰ); (b) case (Ⅱ)(i); (c) case (Ⅱ)(ii), where the red dot represents the positive real root, the light blue and the blue curves of fig. (a) represent the cases of $\varDelta=0$ and $\varDelta < 0$, respectively

图  3  平衡点的存在情况和零斜率线图： (a) 植被生物量$n$随着参数$p$的变化；(b) 在w-n平面上零斜率线$f_{1}(n,w)=0$(紫色/洋红色)和$f_{2}(n,w)=0$(橘色)形成的交点(黑色实心点)，其中$E_{0}$和$E_{{\rm{u}}}$表示植被灭绝平衡点和植被生存平衡点，参数$\gamma=1.6$，$\sigma=0.8$，$\mu=0.2$，$b=0.2$

Figure  3.  The existence of equilibria and zero-slope diagrams: (a) vegetation biomass $n$ vs. $p$; (b) the intersection (black solid points) formed by zero-slope line $f_{1}(n,w)=0$ (purple/magenta) and $f_{2}(n,w)=0$ (orange) on $w{\text{-}}n$ plane, where $E_{0}$ and $E_{{\rm{u}}}$ are the vegetation extinction equilibrium points and the vegetation existence equilibrium points, $\gamma=1.6$，$\sigma=0.8$，$\mu=0.2$，$b=0.2$

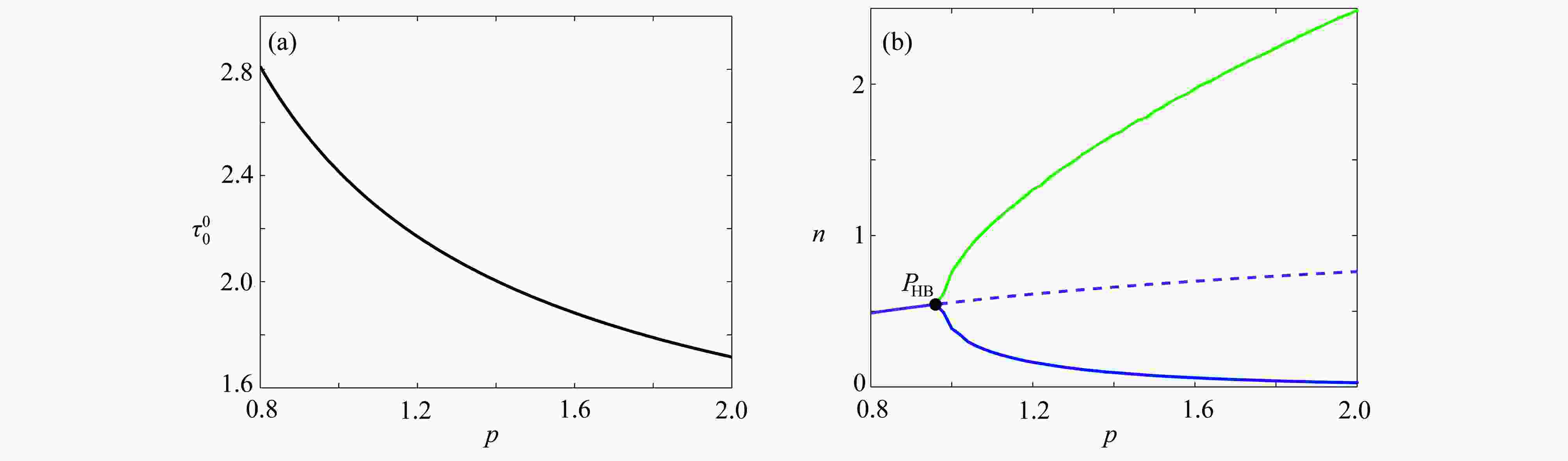
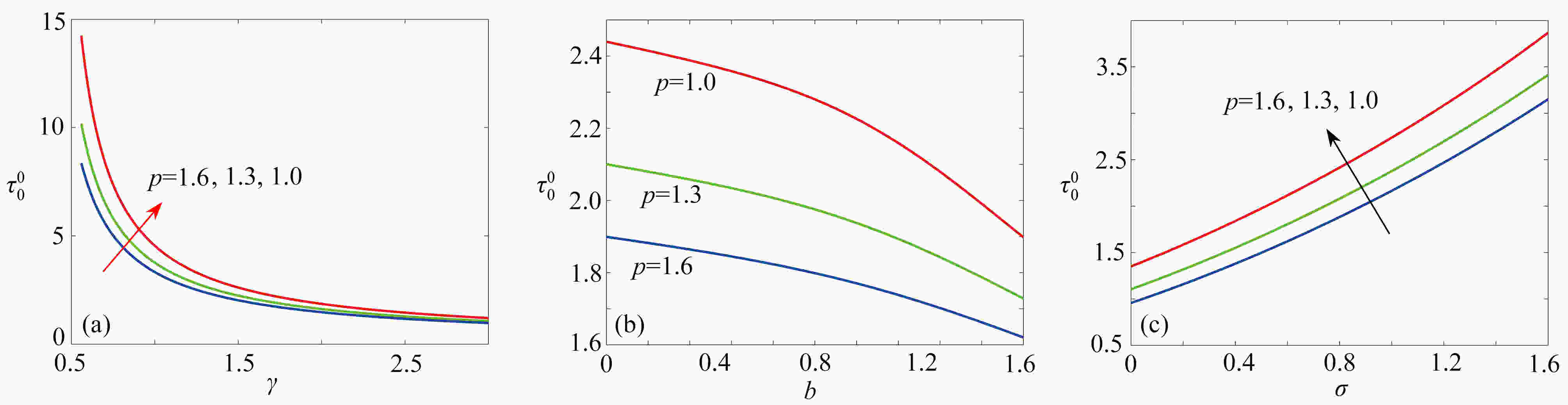
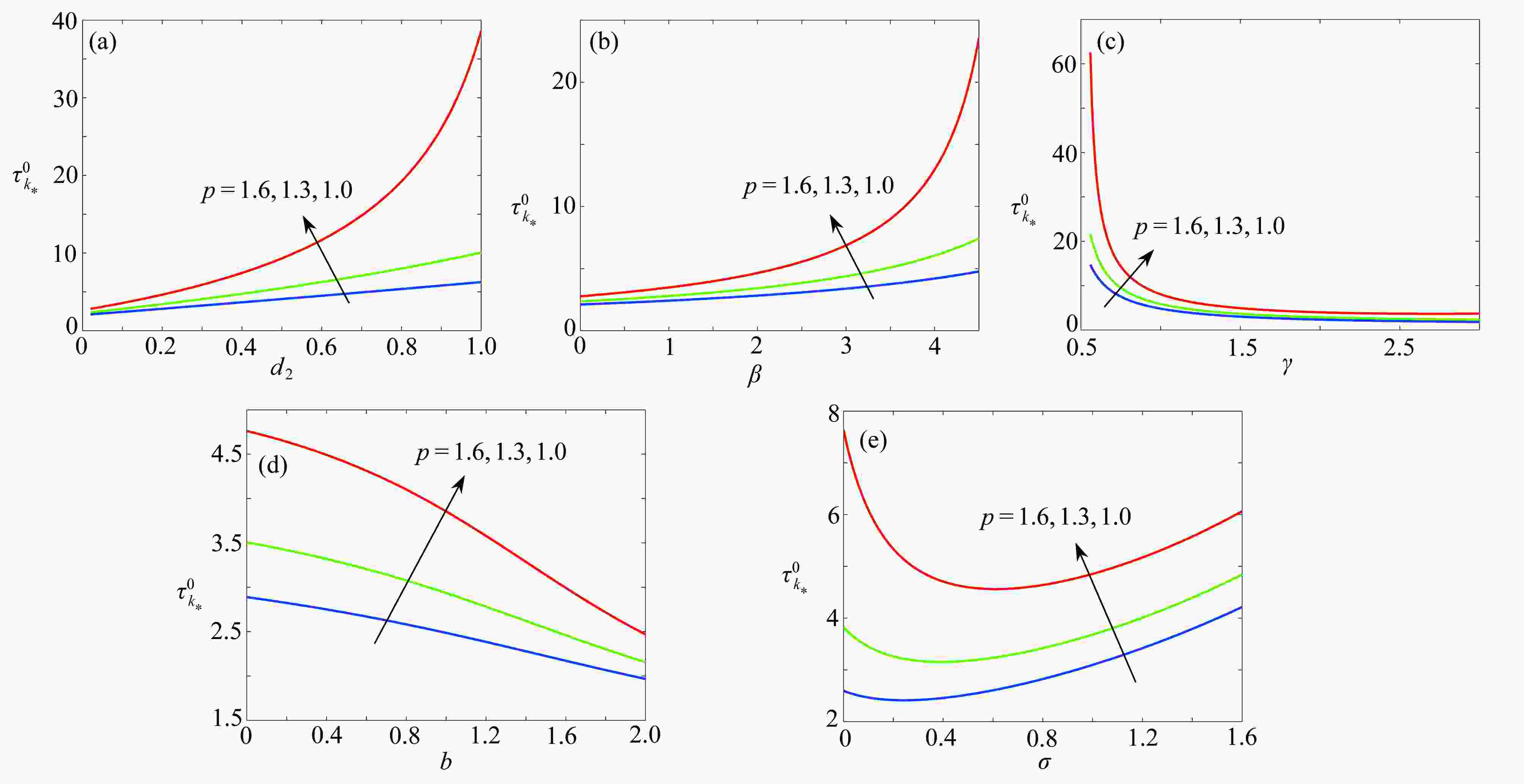
图  4  临界时滞$\tau_{0}^{0} $和植被生物量随参数p的变化情况： (a) $\tau_{0}^{0}$随参数$p$的变化情况；(b) $(p,n)$平面上的单参数分支图，参数$\sigma=0.8$，$\mu=0.2$，$b=0.2$，$\gamma=1.6$ ，$\tau=3$

Figure  4.  The changes of the critical delay $\tau_{0}^{0} $ and the vegetation biomass with parameter p: (a) the variation of $\tau_{0}^{0}$ with $p$; (b) bifurcation diagram in $(p,n)$ plane for $\sigma=0.8$, $\mu=0.2$, $b=0.2$, $\gamma=1.6$ and $\tau=3$

图  5  非空间系统(2)解的数值模拟： (a) $\tau=1$；(b) $\tau=3$；(c) 相图

Figure  5.  Numerical simulation of the solution of non-spatial system (2): (a) $\tau=1$; (b) $\tau=3$; (c) the phase diagram

图  6  对于$p=1.0, 1.3, 1.6$，$\tau_{0}^{0}$随着$\gamma$, $b$, $\sigma$的变化情况，其他参数为$\sigma=0.8$，$\mu=0.2$，$b=0.2$，$\gamma=1.6$

Figure  6.  The variations of $\tau_{0}^{0}$ with $\gamma$, $b$, $\sigma$ for $p=1.0, 1.3, 1.6$, with other parameters of $\sigma=0.8$, $\mu=0.2$, $b=0.2$, $\gamma=1.6$

图  7  $n(x,t)$的时空演化图：(a) $\tau=1$；(b) $\tau=4.8$；(c) 截取图(b)形成的部分图；(d) 图(c)的二维时空图

Figure  7.  The time series of $n(x,t)$: (a) $\tau=1$; (b) $\tau=4.8$; (c) the partial graph cut out of fig. (b); (d) the 2D spatiotemporal graph of fig. (c)

图  8  对于不同的$k$和$\beta$，$\tau_{k_{*}}^{0}$随着参数$p$的变化

Figure  8.  The variations of $\tau_{k_{*}}^{0}$ with $p$ for different $k$ and $\beta$ values

图  9  对于不同的参数$p$，$\tau_{k_{*}}^{0}$随着$d_{2}$，$\beta$，$\gamma$，$b$，$\sigma$的变化情况

Figure  9.  The variations of $\tau_{k_{*}}^{0}$ with $d_{2}$, $\beta$, $\gamma$, $b$, $\sigma$ for different $p$ values

图  10  周期振荡模式的敏感性分析，参数$\sigma=0.8$，$\mu=0.2$，$b=0.2$，$\gamma=1.6$，$d_{1}=0.02$，$d_{2}=0.2$，$\beta=2$，$k=2$

Figure  10.  Sensitivity analysis of periodic oscillation patterns with parameters of $\sigma=0.8$, $\mu=0.2$, $b=0.2$, $\gamma=1.6$, $d_{1}=0.02$, $d_{2}=0.2$, $\beta=2$, $k=2$