A Space-Time Polynomial Collocation Method for Solving 3D Burgers Equations
-
摘要:
Burgers方程是一类应用广泛的非线性偏微分方程，方程中的非线性项难以处理。该文提出一种新的时空多项式配点法——多项式特解法求解三维Burgers方程。求解过程分为两步：第一步，对三维Burgers方程中的线性导数项(包括时间导数项)，求出相应的多项式特解。第二步，将求出的多项式特解作为基函数，对三维Burgers方程中剩余的非线性项进行迭代求解。与时空多项式函数作为基函数对三维Burgers方程进行直接求解相比，该算法简单易行，得到的近似解精度非常高，算法极其稳定，对于教学过程中提高学生的编程能力，加深对高维Burgers方程的理解能力以及Burgers方程的实际应用具有重要意义。
Abstract:As a class of nonlinear partial differential equations, the Burgers equations are widely used in various fields. A new space-time polynomial collocation method was presented for particular solutions to 3D Burgers equations. The basic process was divided into 2 steps. The 1st step is to find the polynomial particular solutions of the linear differential operator terms (including the time differential term) in the governing equation. The 2nd step is to solve the nonlinear term of the 3D Burgers equation iteratively. The proposed method is simple and easy to program. The approximate solution has high accuracy. Especially, the stability of the method is excellent, which improves the programming simplicity and deepens the understanding of high-dimensional Burgers equations and the practical application.
-
Key words:
- collocation method /
- polynomial solution method /
- Burgers equation /
- MATLAB program
-
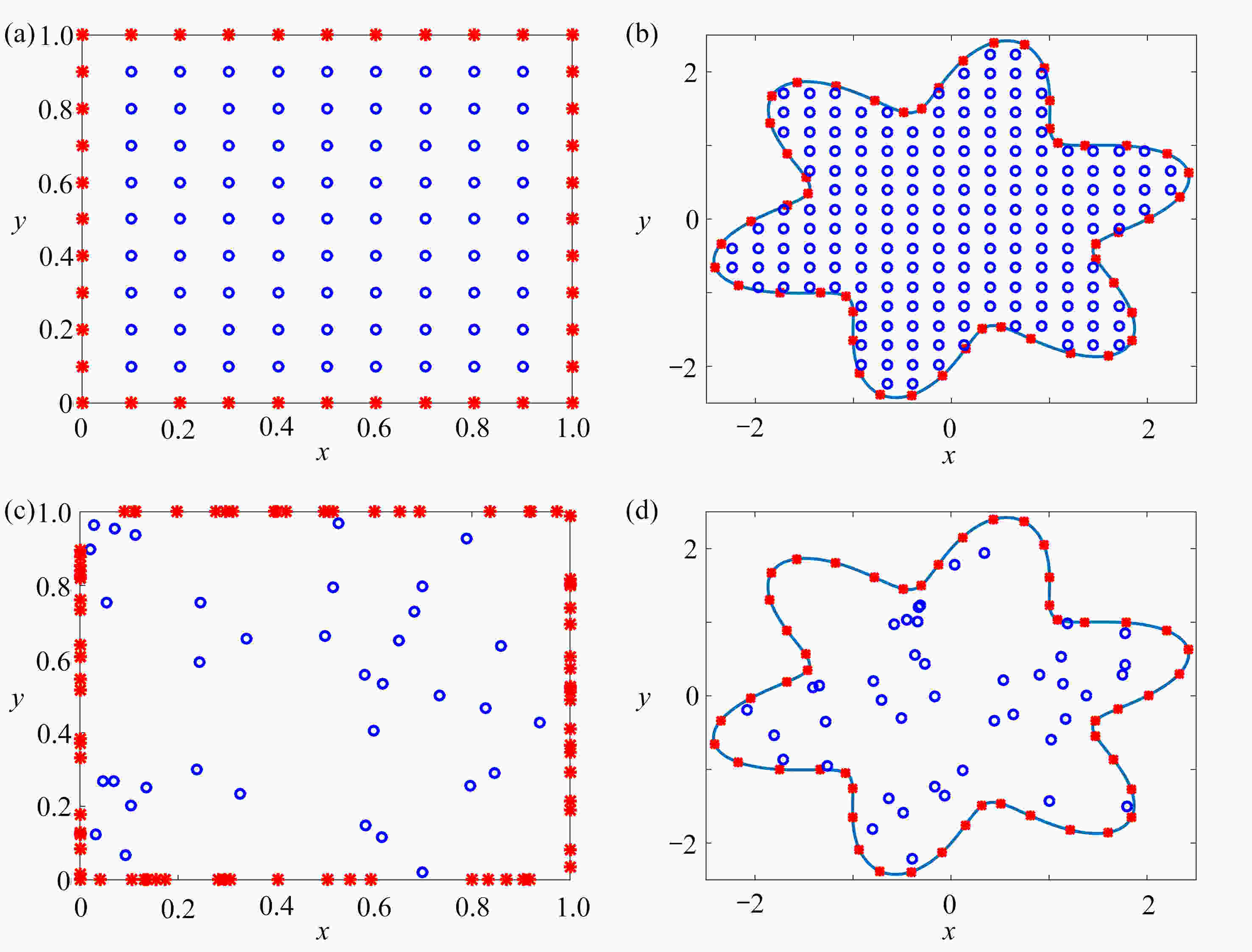
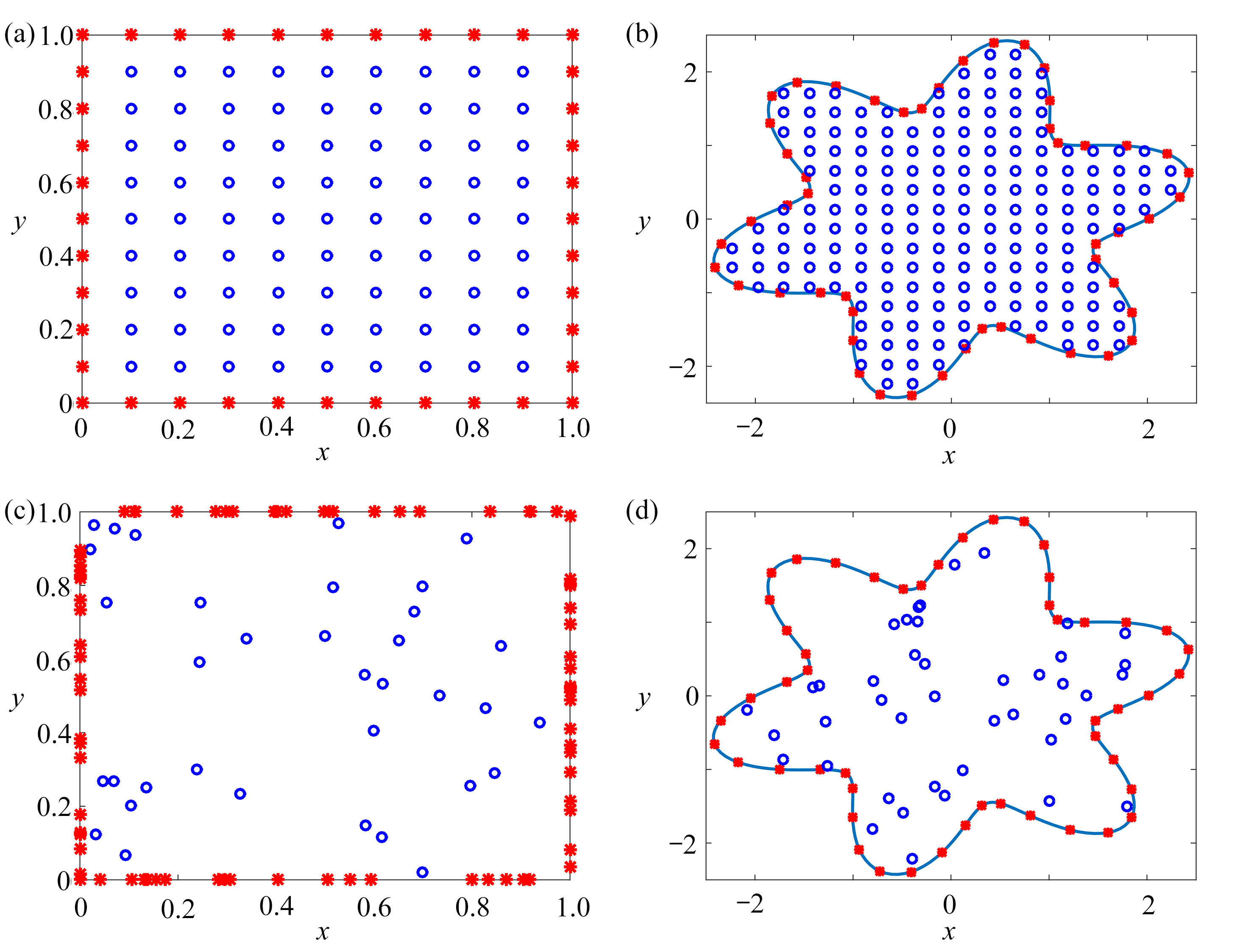
图 1 配点图：(a) 正方形区域规则取点；(b) 星形区域规则取点；(c) 正方形区域随机取点；(d) 星形区域随机取点(篮圈：内点；红星：边界点)
Figure 1. The collocation point diagram: (a) the regular domain with regular points; (b) the irregular domain with regular points; (c) the regular domain with random points; (d) the irregular domain with random points (blue circles: interior collocation points; red stars: boundary collocation points)
图 2 时空区域中星形区域随机取点（篮圈：内点；红星：边界点）
注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同。
Figure 2. An irregular domain with random points in the space-time domain (blue circles: interior collocation points; red stars: boundary collocation points)
图 3 空间求解区域：(a) 正方体区域；(b) bumpy-shaped区域
Figure 3. The spatial solution domains: (a) the cubic domain; (b) the bumpy-shaped domain
图 6
${\tau}=2$ 时，正方体区域上系数矩阵的条件数：(a) 多项式特解系数矩阵的条件数；(b) 多项式基函数系数矩阵的条件数Figure 6. Matrix condition numbers of the cubic domain for
${\tau}=2$ : (a) the condition number of polynomial particular solutions; (b) the condition number of polynomial basis functions表 1
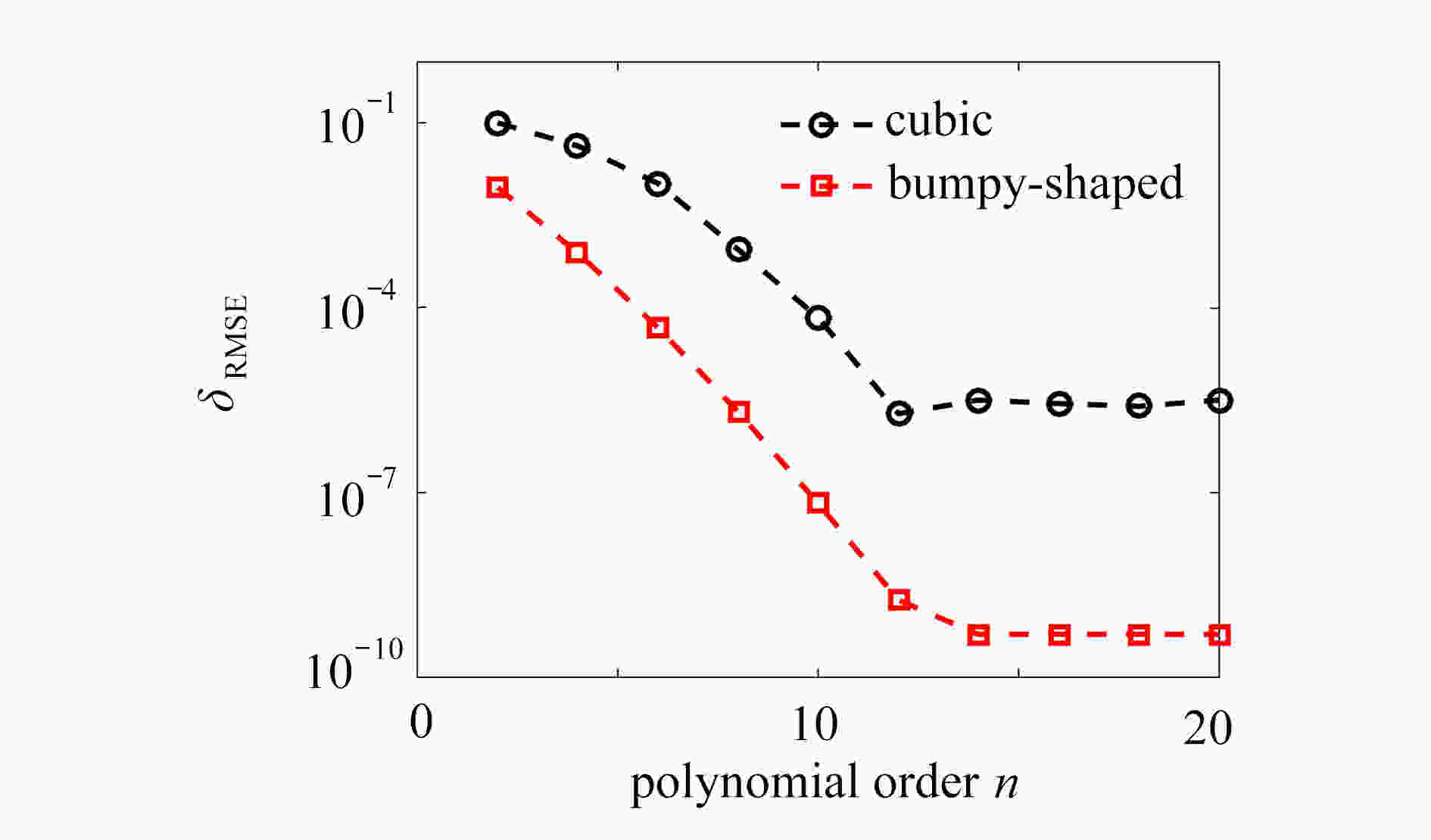
$n_{{{\rm{i}}}}=3\;819,\;n_{{{\rm{d}}}}=5\;220,\;n_{{{\rm{t}}}}=1\;919,\;{\tau}=1$ 时，两种区域多项式特解的平方根误差Table 1. The RMSE with
$n_{{{\rm{i}}}}=3\;819,\; n_{{{\rm{d}}}}=5\;220,\; n_{{{\rm{t}}}}=1\;919,\; {\tau}=1$ for cubic and bumpy-shaped domainsorder cubic ${\delta_{\rm{RMSE1}}}$ bumpy-shape ${\delta_{\rm{RMSE2}}}$ CPU time t/s 4 7.65E−4 1.21E−4 0.375 6 4.74E−5 1.84E−6 1.886 8 2.42E−6 5.13E−9 10.290 10 1.31E−7 5.13E−10 38.707 
下载: 导出CSV
表 2
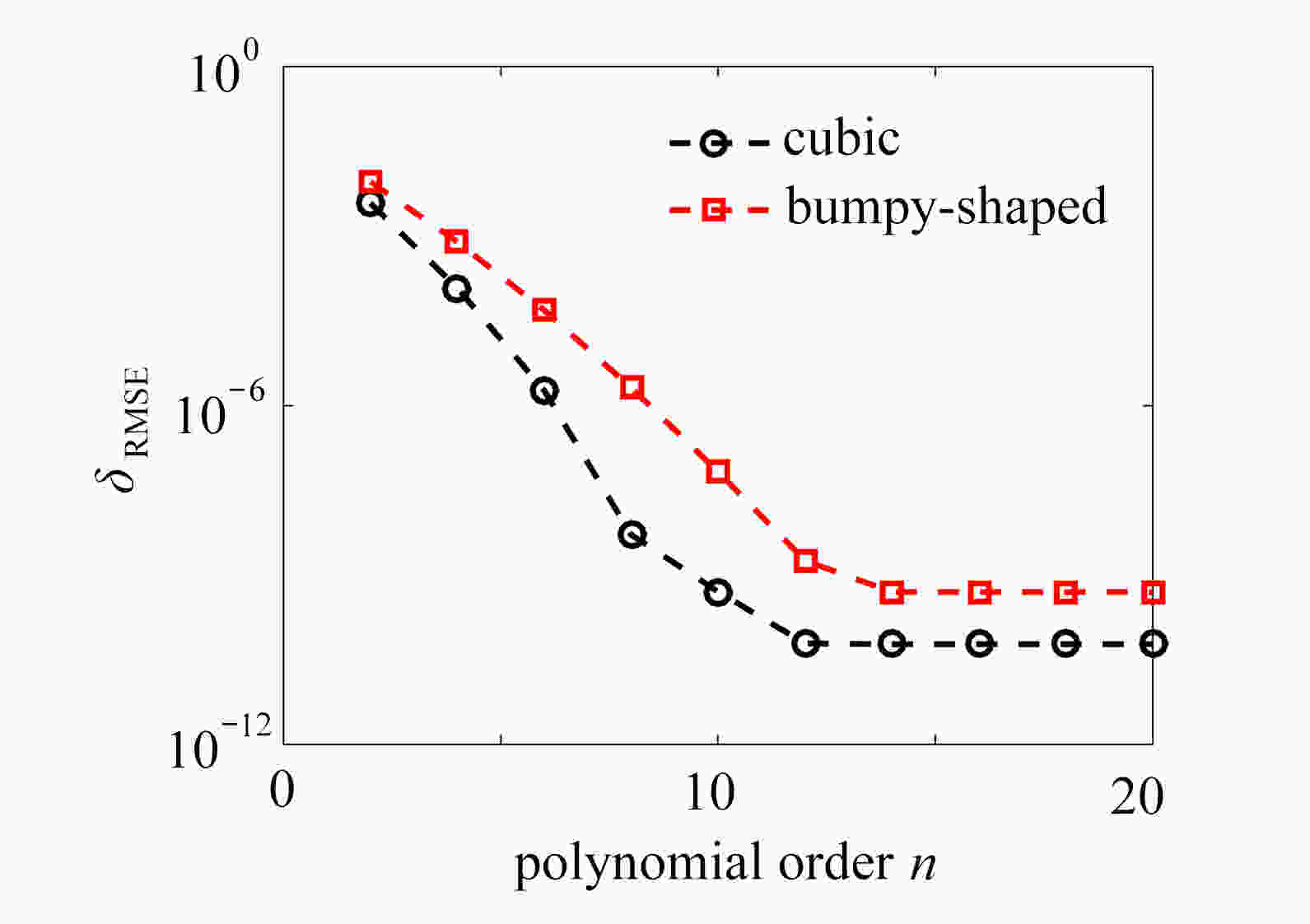
$n_{{{\rm{i}}}}=3\;819,\;n_{{{\rm{d}}}}=5\;220,\;n_{{{\rm{t}}}}=1\;919,\;{\tau}=1$ 时，两种区域多项式基函数的平方根误差Table 2. The RMSE with
$n_{{{\rm{i}}}}=3\;819,\; n_{{{\rm{d}}}}=5\;220,\; n_{{{\rm{t}}}}=1\;919, \;{\tau}=1$ for cubic and bumpy-shaped domainsorder cubic $ {\delta_{\rm{RMSE1} } }$ bumpy-shape $ {\delta_{\rm{RMSE2} } }$ CPU time t/s 4 2.14E−2 8.22E−2 0.454 6 2.04E−2 7.70E−2 3.418 8 2.02E−2 5.53E−2 23.440 10 2.00E−2 5.51E−2 126.793
下载: 导出CSV
表 3
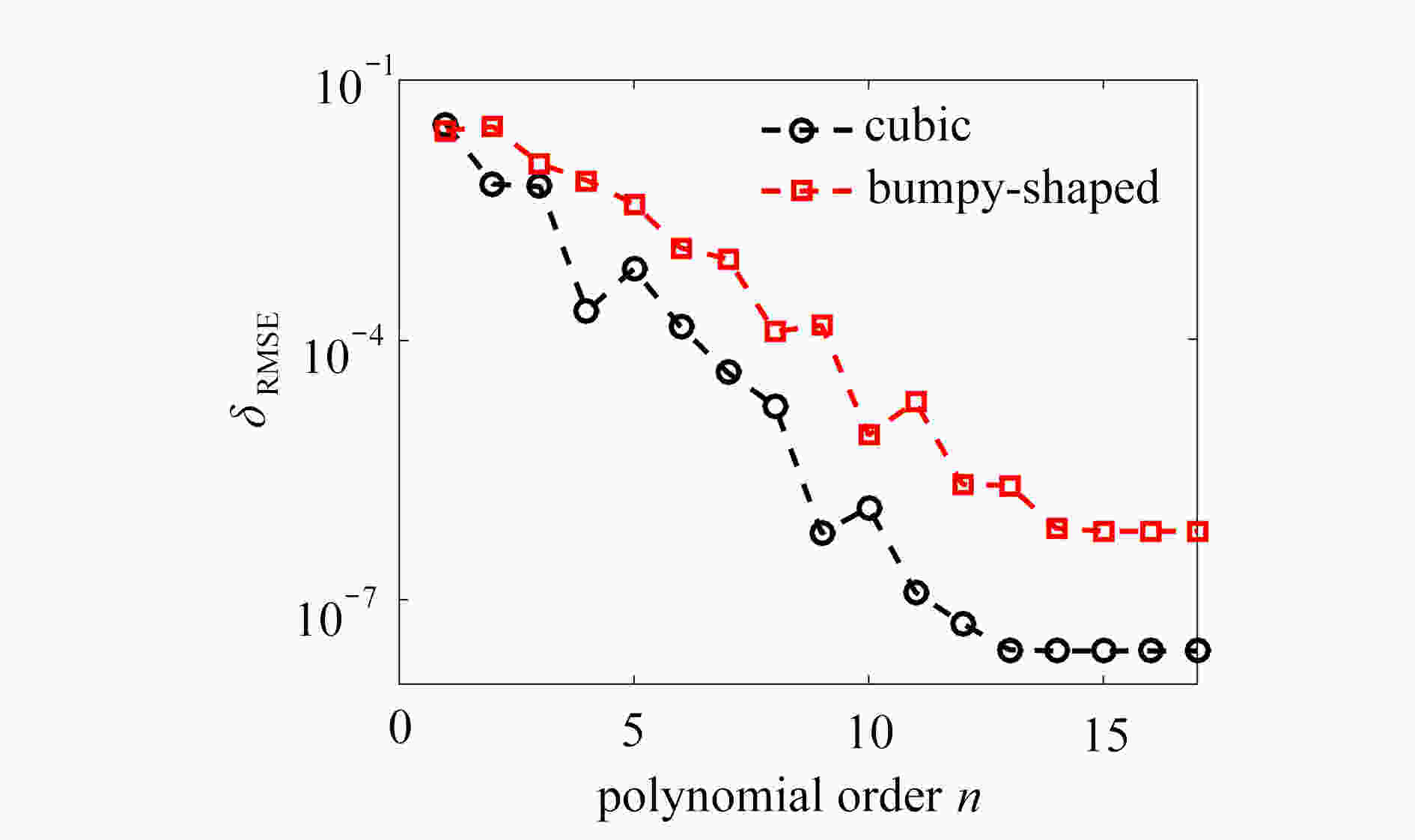
$n_{{{\rm{i}}}}=3\;819,\;n_{{{\rm{d}}}}=5\;220,\;n_{{{\rm{t}}}}=1\;919,\;\mu=0.5$ 时，两种区域多项式基函数的平方根误差和计算所需时间Table 3. The RMSE with
$n_{{{\rm{i}}}}=3\;819, n_{{{\rm{d}}}}=5\;220, n_{{{\rm{t}}}}=1\;919, \mu=0.5$ for cubic and bumpy-shaped domainsorder cubic $\delta_{{\rm{RMSE}}1}$ bumpy-shape $\delta_{{\rm{RMSE}}2}$ CPU time t/s 4 4.44E−3 3.49E−2 0.590 6 4.40E−3 9.85E−3 2.367 8 4.35E−3 5.78E−3 9.780 10 4.32E−3 7.27E−3 37.786
下载: 导出CSV
-
[1] BURGER J M. A mathematical model illustrating the theory of turbulence[J]. Advances in Applied Mechanics, 1948, 1: 171-199. [2] HOPF E. The partial differential equation $u_t + uu_x =\mu_xx $ [J]. Communications on Pure and Applied Mathematics, 1950, 3(3): 201-230. doi: 10.1002/cpa.3160030302[3] HASSANIEN I A, SALAMA A A, HOSHAM H A J. Fourth-order finite difference method for solving Burgers’ equation[J]. Applied Mathematics and Computation, 2005, 170(2): 781-800. doi: 10.1016/j.amc.2004.12.052 [4] COLE J D. On a quasi-linear parabolic equation occurring in aerodynamics[J]. Quarterly of Applied Mathematics, 1951, 9(3): 225-236. doi: 10.1090/qam/42889 [5] 包立平, 胡玉博, 吴立群. 具有初值间断的Burgers方程奇摄动解[J]. 应用数学和力学, 2020, 41(7): 807-816BAO Liping, HU Yubo, WU Liqun. Singularly perturbed solutions of Burgers equations with initial value discontinuities[J]. Applied Mathematics and Mechanics, 2020, 41(7): 807-816.(in Chinese) [6] 包立平, 洪文珍. 一维弱噪声随机Burgers方程的奇摄动解[J]. 应用数学和力学, 2018, 39(1): 113-122.BAO Liping, HONG Wenzhen. Singular perturbation solutions to 1D stochastic Burgers equations under weak noises[J]. Applied Mathematics and Mechanics, 2018, 39(1): 113-122. (in Chinese) [7] 朱位秋. 几类非线性系统对白噪声参激与/或外激平稳响应的精确解[J]. 应用数学和力学, 1990, 11(2): 155-164ZHU Weiqiu. Exact solutions for stationary responses of several classes of nonlinear systems to parametric and/or external white noise excitations[J]. Applied Mathematics and Mechanics, 1990, 11(2): 155-164.(in Chinese) [8] GULSU M. A finite difference approach for solution of Burgers’ equation[J]. Applied Mathematics and Computation, 2006, 175(2): 1245-1255. doi: 10.1016/j.amc.2005.08.042 [9] CALDWELL J, WANLESS P. Solution of Burgers’ equation for large Reynolds number using finite elements with moving nodes[J]. Applied Mathematical Modelling, 1987, 11(3): 211-214. doi: 10.1016/0307-904X(87)90005-9 [10] TURGUT Z, ASLAN Y. The semi-approximate approach for solving Burgers’ equation with high Reynolds number[J]. Applied Mathematics and Computation, 2005, 163(1): 131-145. doi: 10.1016/j.amc.2004.01.032 [11] HASHEMIAN A, SHODJA H M. A meshless approach for solution of Burgers’ equation[J]. Journal of Computational and Applied Mathematics, 2008, 220(1): 226-239. [12] ZHANG X H, OUYANG J, ZHANG L. Element-free characteristic Galerkin method for Burgers’ equation[J]. Engineering Analysis With Boundary Elements, 2009, 33(3): 356-362. doi: 10.1016/j.enganabound.2008.07.001 [13] CHEN R, WU Z. Applying multiquadric quasi-interpolation to solve Burgers’ equation[J]. Applied Mathematics and Computation, 2006, 172(1): 472-484. doi: 10.1016/j.amc.2005.02.027 [14] HON Y C, MAO X Z. An efficient numerical scheme for Burgers’ equation[J]. Applied Mathematics and Computation, 1999, 95(1): 37-50. [15] MOHAMMADI M, MOKHTARI R, PANAHIPOUR H. A Galerkin-reproducing kernel method: application to the 2D nonlinear coupled Burgers’ equations[J]. Engineering Analysis With Boundary Elements, 2013, 37(12): 1642-1652. doi: 10.1016/j.enganabound.2013.09.005 [16] ZHANG X, TIAN H, CHEN W. Local method of approximate particular solutions for two-dimensional unsteady Burgers’ equations[J]. Computers and Mathematics With Applications, 2014, 66(12): 2425-2432. doi: 10.1016/j.camwa.2013.10.009 [17] ZHENG H, ZHANG C, WANG Y. Band structure computation of in-plane elastic waves in 2D phononic crystals by a meshfree local RBF collocation method[J]. Engineering Analysis With Boundary Elements, 2016, 66: 77-90. doi: 10.1016/j.enganabound.2016.01.012 [18] TEZDUYAR T E, SATHE S, KEEDY R. Space-time finite element techniques for computation of fluid-structure interactions[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(17/18): 2002-2027. doi: 10.1016/j.cma.2004.09.014 [19] KLAIJ C M, DER VAN J J, DER VAN H V. Space-time discontinuous Galerkin method for the compressible Navier-Stokes equations[J]. Journal of Computational Physics, 2006, 217(2): 589-611. doi: 10.1016/j.jcp.2006.01.018 [20] MOHAMMED H, AHMED N, ABDELLATIF C. Space-time localized radial basis function collocation method for solving parabolic and hyperbolic equations[J]. Engineering Analysis With Boundary Elements, 2016, 67: 152-163. doi: 10.1016/j.enganabound.2016.03.009 [21] DANGAL T R, CHEN C S, LIN J. Polynomial particular solutions for solving elliptic partial differential equations[J]. Computers and Mathematics With Applications, 2017, 73(1): 60-70. doi: 10.1016/j.camwa.2016.10.024 [22] CAO Y H, CHEN C S, ZHENG H. Space-time polynomial particular solutions method for solving time-dependent problems[J]. Numerical Heat Transfer, Part B: Fundamentals, 2020, 77(3): 181-194. doi: 10.1080/10407790.2019.1693199 [23] CAO Y H, LI N, ZHANG Z T. The method of polynomial particular solutions for solving ordinary differential equations[J]. Mathematica Applicata, 2020, 33(2): 295-307. -
计量
- 文章访问数: 798
- HTML全文浏览量: 578
- PDF下载量: 101
- 被引次数: 0
渝公网安备50010802005915号