A Spatial Geometric Nonlinearity Spline Beam Element With Nodal Parameters Containing Strains
-
摘要:
工程中很多细长杆件可以抽象为Euler-Bernoulli梁，分析其动态行为时需要对其进行柔性多体系统动力学建模。以绝对节点坐标参数为代表的几何非线性梁单元解决了大量柔性梁动力学问题，但仍然面临诸如剪切闭锁、节点应力不连续、计算效率低下等问题。鉴于此，以大变形梁虚功率方程为理论基础，建立了转动参数和位移参数间的转换方程，满足Euler-Bernoulli梁变形耦合关系，推导了这种情况下可描述梁几何非线性效应的广义应变；保证应力连续的情况下，采用样条插值实现单元间缩减自由度式组装；将边界节点部分参数替换为轴向应变和截面曲率，得到了更加准确简洁的施加外力的约束方式；对梁结构的运动方程进行降噪处理，来滤除高频分量，提高求解效率；并通过数值算例验证了所提单元的有效性。
Abstract:Many slender rods in engineering can be modeled as Euler-Bernoulli beams. For the analysis of their dynamic behaviors, it is necessary to establish the dynamic models for the flexible multi-body systems. Geometric nonlinear elements with absolute nodal coordinates help solve a large number of dynamic problems of flexible beams, but they still face such problems as shear locking, nodal stress discontinuity and low computation efficiency. Based on the theory of large deformation beams’ virtual power equations, the functional formulas between displacements and rotation angles at the nodes were established, which can satisfy the deformation coupling relationships. The generalized strains to describe geometric nonlinear effects in this case were derived. Some parameters of boundary nodes were replaced by axial strains and sectional curvatures to obtain a more accurate and concise constraint method for applying external forces. To improve the numerical efficiency and stability of the system’s motion equations, a model-smoothing method was used to filter high frequencies out of the model. The numerical examples verify the rationality and effectiveness of the proposed element.
-
图 9 悬臂梁受集中力矩作用的位移ux曲线
Figure 9. End displacement ux of the cantilever beam with an end bending moment
图 10 悬臂梁受集中力矩作用的位移uy曲线
Figure 10. End displacement uy of the cantilever beam with an end bending moment
图 11 悬臂梁在不同弯矩作用下的变形曲线
Figure 11. Large deformation curves of the cantilever beam under different bending moments
图 12 悬臂梁受集中力矩的位移曲线
Figure 12. The displacements of the cantilever beam with an end bending moment
图 14 旋转柔性梁初始状态及动态载荷
Figure 14. The initial state and dynamic loads of the rotating flexible beam
图 15 旋转梁自由端的位移-时间曲线
Figure 15. Displacement-time curves at the free end of the rotating beam
图 16 时刻15 s和30 s时，旋转梁的广义应变
Figure 16. Generalized strains of the rotating beam at 15 s and 30 s
图 17 “L”形悬臂梁初始状态及动态载荷
Figure 17. The initial state and dynamic loads of the L-shaped cantilever beam
图 18 “L”形悬臂梁自由端与弯头处的位移曲线
Figure 18. The displacement curves at the free end and the elbow of the L-shaped cantilever beam
图 19 “L”形悬臂梁自由端节点的广义应变
Figure 19. Generalized strains at the free end of the L-shaped cantilever beam
图 21 空间组合梁结构受力端位移
Figure 21. Displacements at the end of the spatial structure composed of beams
表 1 效率比较（柔性单摆机构）
Table 1. Efficiency comparison (for the flexible pendulum mechanism)
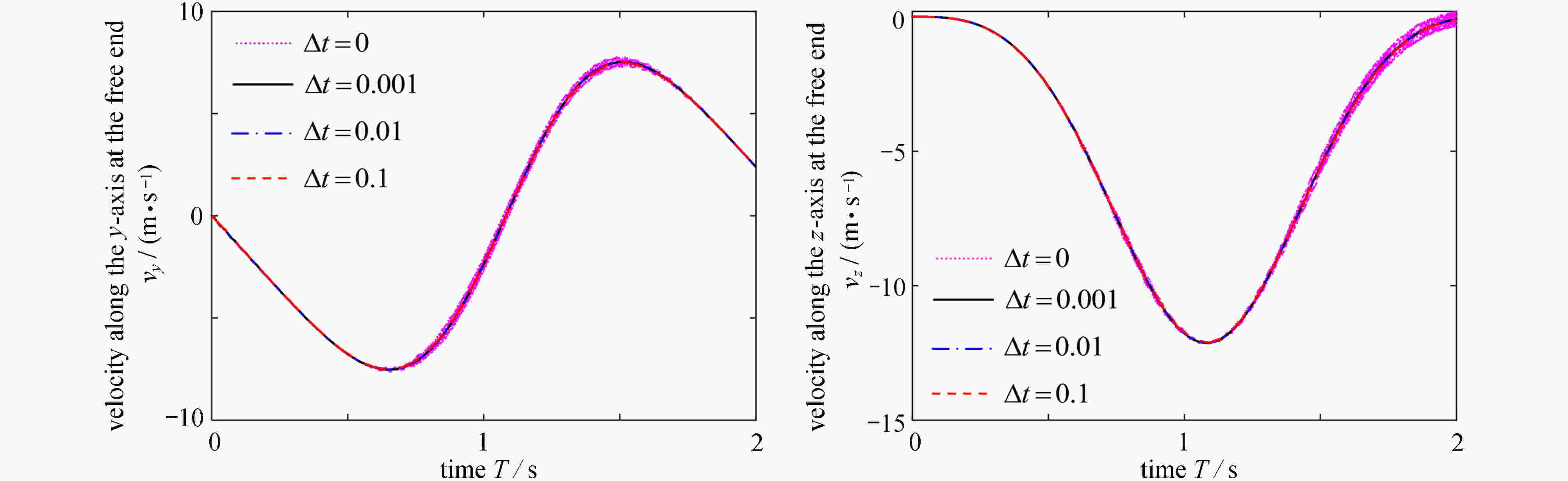
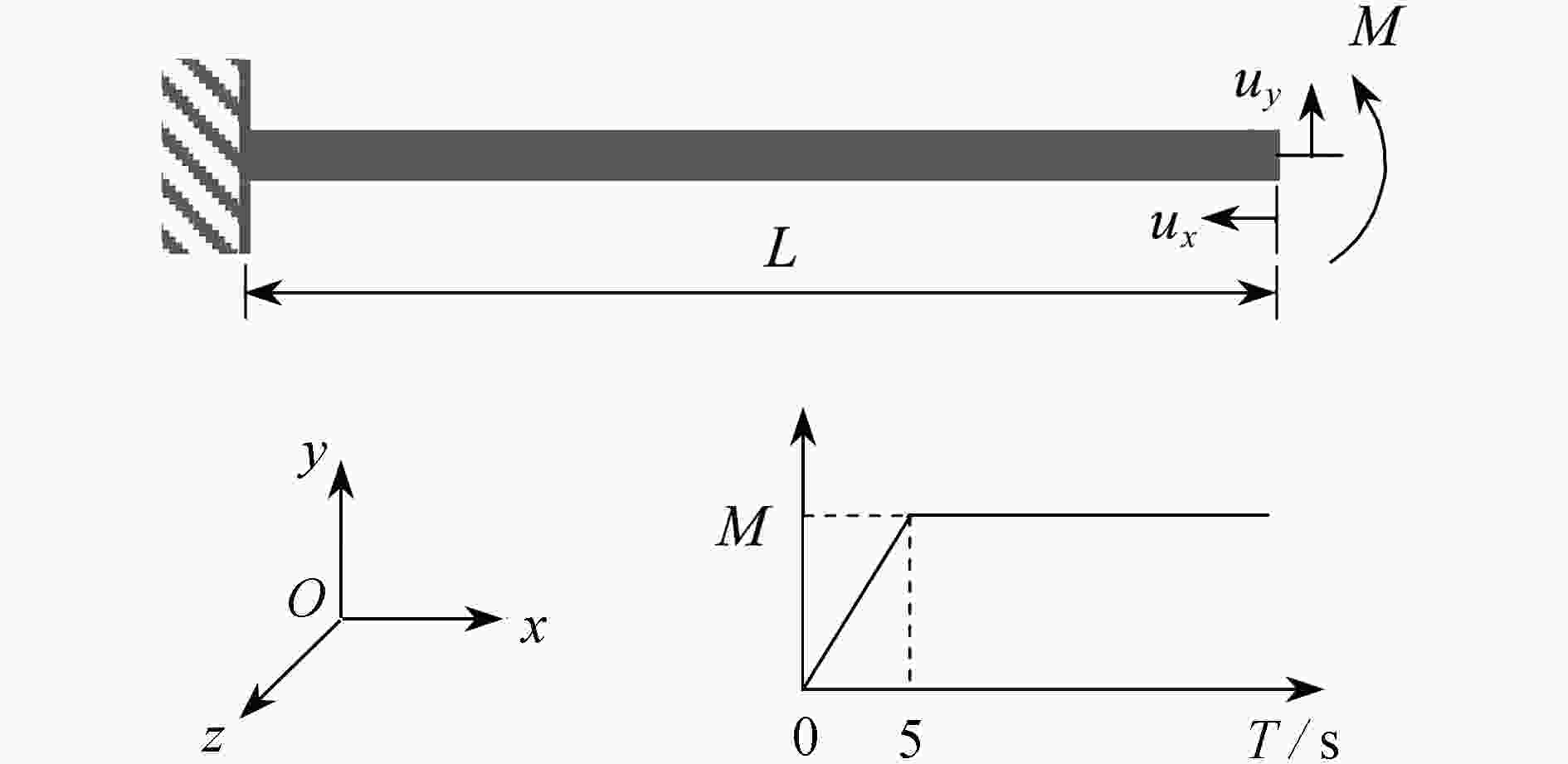
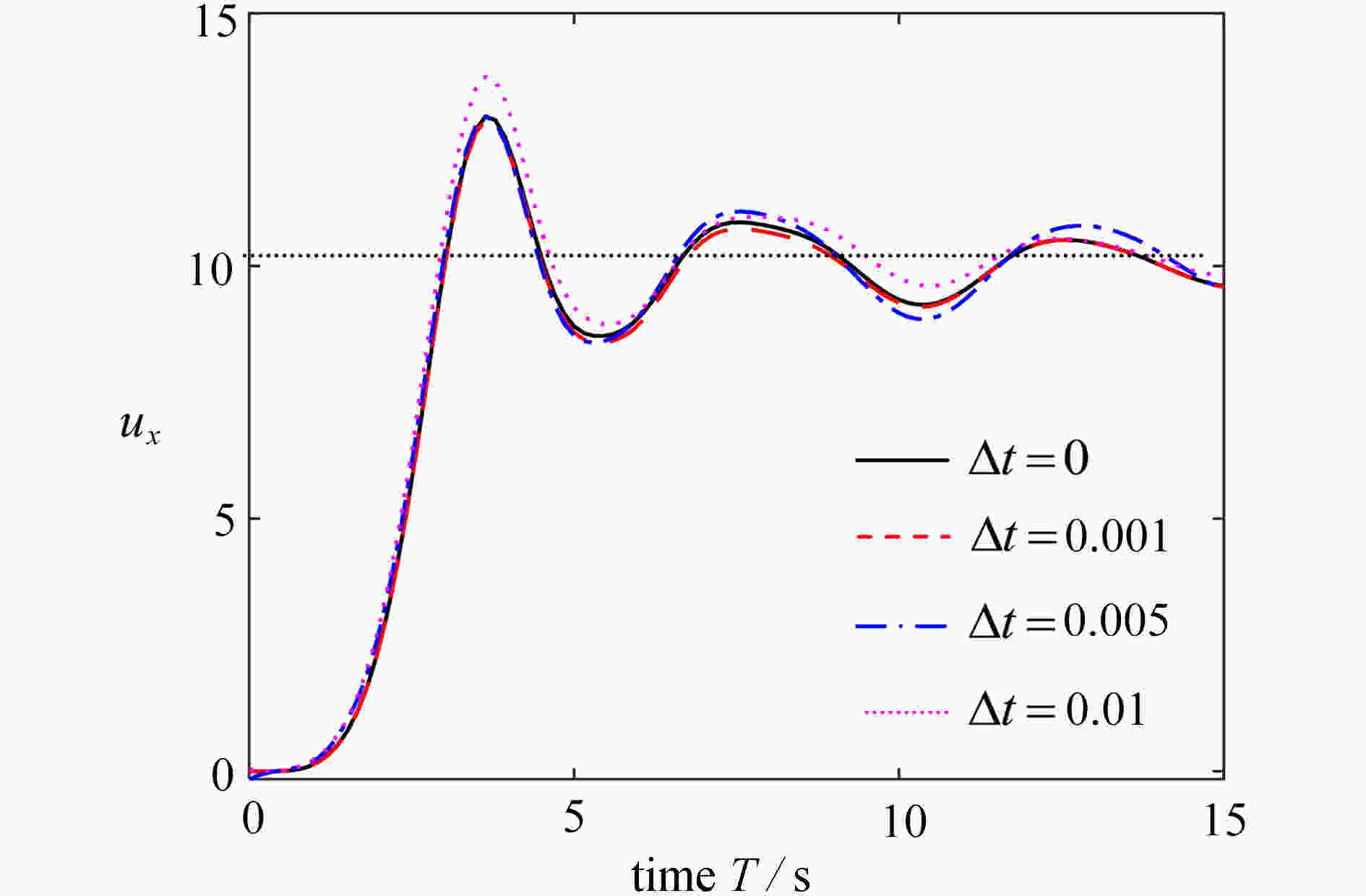
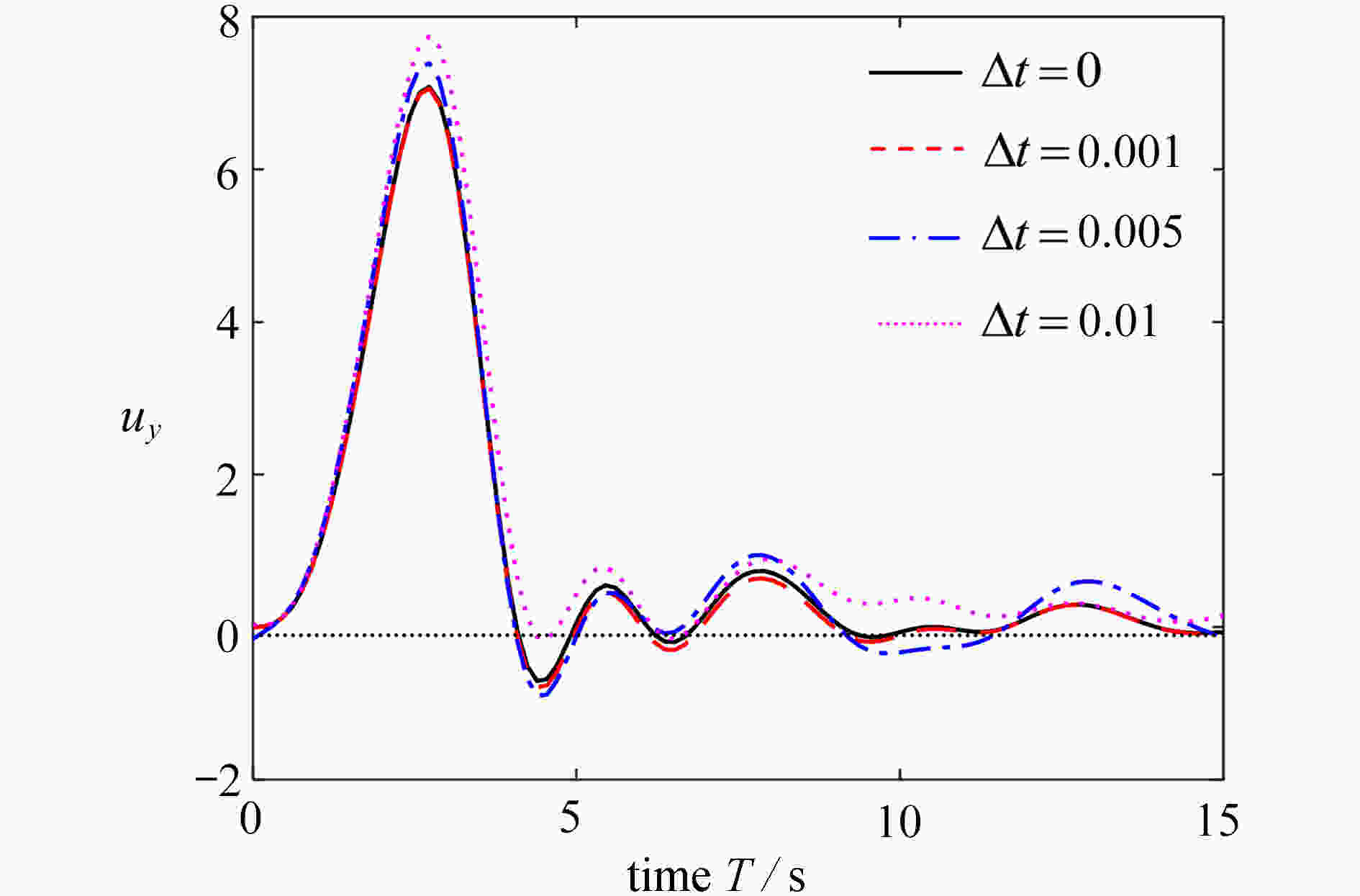
smoothing factor Δt 0.1 0.01 0.001 0 simulation time T/s 2 12 100 6 854 
下载: 导出CSV
表 2 悬臂梁受集中力矩 M=2πL−1EI 时选取不同光滑因子仿真用时
Table 2. The simulation time of different smoothing factors for the cantilever beam subjected to an end bending load M=2πL−1EI
smoothing factor Δt 0.01 0.005 0.001 0 simulation time T/s 285 526 982 3 653
下载: 导出CSV
表 3 悬臂梁不同剪力作用下平衡状态时竖向位移
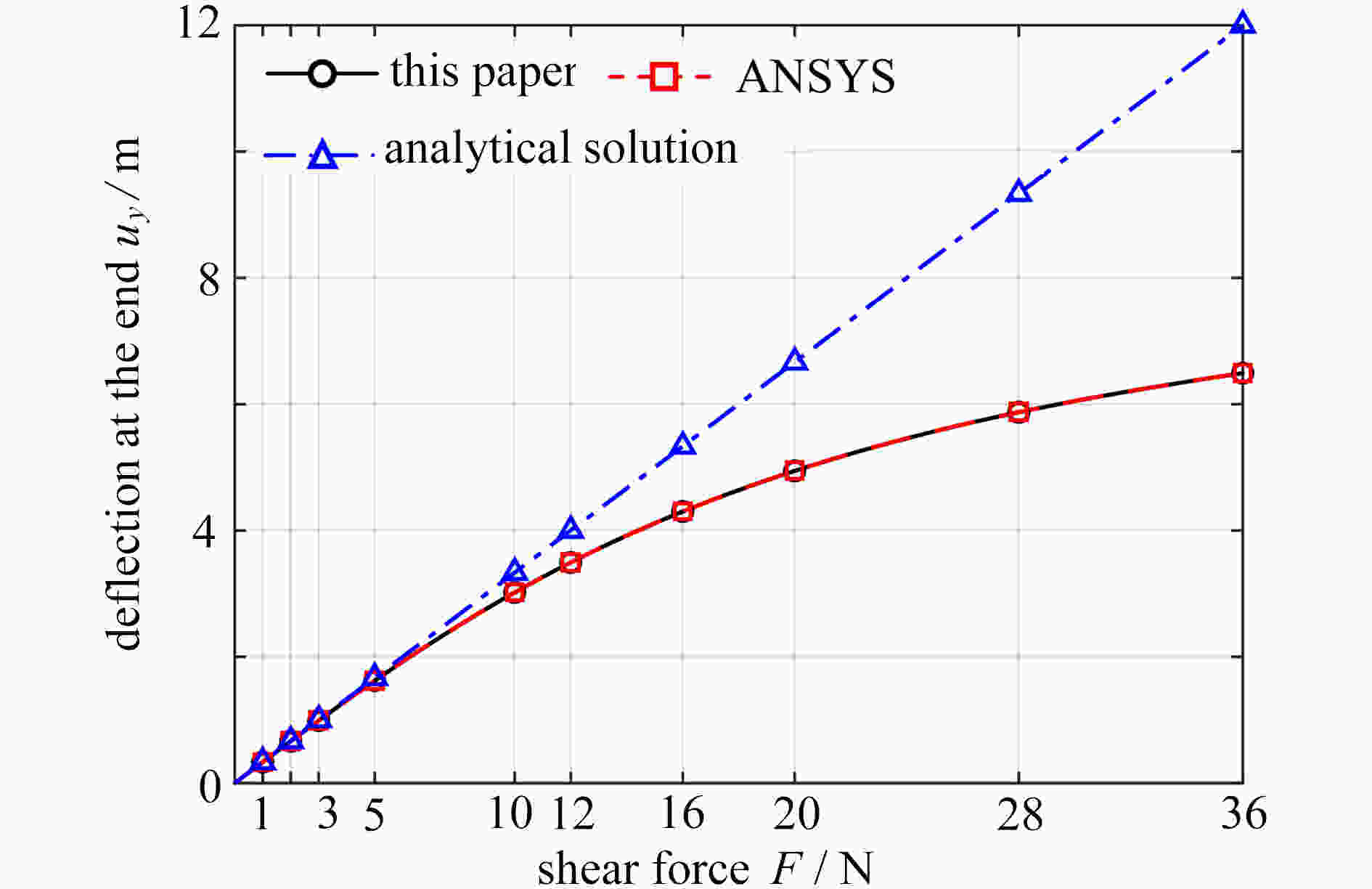
Table 3. Equilibrium deflections at the cantilever beam end under different shear forces
F/N ${u_y}$/m ANSYS analytical solution ${u_y}$/m error εw/% ${u_y}$/m error εw/% 1 0.3330 0.3334 0.13 0.3333 0.11 2 0.6637 0.6642 0.08 0.6667 0.45 3 0.9900 0.9900 0 1.0000 1.00 5 1.6217 1.6215 0.01 1.6667 2.77 10 3.0192 3.0194 0.01 3.3333 10.4 12 3.4931 3.4935 0.01 4.0000 14.5 16 4.3000 4.3005 0.01 5.3333 24.0 20 4.9435 4.9444 0.02 6.6667 34.9 28 5.8725 5.8739 0.02 9.3333 58.9 36 6.4912 6.4931 0.03 12.0000 84.9
下载: 导出CSV
-
[1] LI L, ZHANG D G, GUO Y B. Dynamic modeling and analysis of a rotating flexible beam with smart ACLD treatment[J]. Composites Part B: Engineering, 2017, 131: 221-236. doi: 10.1016/j.compositesb.2017.07.050 [2] LE T N, BATTINI J M, HJIAJ M. A consistent 3D corotational beam element for nonlinear dynamic analysis of flexible structures[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 269: 538-565. doi: 10.1016/j.cma.2013.11.007 [3] 王单, 王健. 重力载荷作用下柔性梁的结构变形与承载力分析[J]. 应用数学和力学, 2021, 42(6): 611-622WANG Dan, WANG Jian. Analysis of deformation and bearing capacity of flexible beams under gravitational loads[J]. Applied Mathematics and Mechanics, 2021, 42(6): 611-622.(in Chinese) [4] 周兰伟, 陈国平, 孙东阳. 高速旋转柔性梁刚柔耦合动力学分析[J]. 振动与冲击, 2017, 36(5): 142-146 doi: 10.13465/j.cnki.jvs.2017.05.022ZHOU Lanwei, CHEN Guoping, SUN Dongyang. Rigid-flexible coupled dynamic analysis for a high-speed spinning flexible beam[J]. Journal of Vibration and Shock, 2017, 36(5): 142-146.(in Chinese) doi: 10.13465/j.cnki.jvs.2017.05.022 [5] 黄永安, 邓子辰, 姚林晓. 考虑大变形的刚-柔耦合旋转智能结构动力学分析[J]. 应用数学和力学, 2007, 28(10): 1203-1212HUANG Yongan, DENG Zichen, YAO Linxiao. Dynamic analysis of a rotating rigid-flexible coupled smart structure with large deformation[J]. Applied Mathematics and Mechanics, 2007, 28(10): 1203-1212.(in Chinese) [6] 孟阳君, 张家生. 杆系结构的大变形几何非线性分析[J]. 铁道科学与工程学报, 2018, 15(8): 2034-2039 doi: 10.19713/j.cnki.43-1423/u.2018.08.017MENG Yangjun, ZHANG Jiasheng. A large deformation geometric nonlinear analysis for frame structure[J]. Journal of Railway Science and Engineering, 2018, 15(8): 2034-2039.(in Chinese) doi: 10.19713/j.cnki.43-1423/u.2018.08.017 [7] 吴庆雄, 陈宝春, 韦建刚. 三维杆系结构的几何非线性有限元分析[J]. 工程力学, 2007, 24(12): 19-24 doi: 10.3969/j.issn.1000-4750.2007.12.004WU Qingxiong, CHEN Baochun, WEI Jiangang. A geometric nonlinear finite element analysis for 3D framed structures[J]. Engineering Mechanics, 2007, 24(12): 19-24.(in Chinese) doi: 10.3969/j.issn.1000-4750.2007.12.004 [8] 叶康生, 陆天天, 袁驷. 结构几何非线性分析中分叉失稳的直接求解[J]. 工程力学, 2011, 28(8): 1-8YE Kangsheng, LU Tiantian, YUAN Si. A direct method for the computation of bifurcation buckling in geometric nonlinear analysis of structures[J]. Engineering Mechanics, 2011, 28(8): 1-8.(in Chinese) [9] WEMPNER G. Finite elements, finite rotations and small strains of flexible shells[J]. International Journal of Solids & Structures, 1969, 5(2): 117-153. [10] BELYTSCHKO T, HSIEH B J. Non-linear transient finite element analysis with convected co-ordinates[J]. International Journal for Numerical Methods in Engineering, 1973, 7(3): 255-271. doi: 10.1002/nme.1620070304 [11] 史加贝, 刘铸永, 洪嘉振. 柔性多体动力学的共旋坐标法[J]. 力学季刊, 2017, 38(2): 23-40 doi: 10.15959/j.cnki.0254-0053.2017.02.002SHI Jiabei, LIU Zhuyong, HONG Jiazhen. The co-rotational formulation for flexible multibody dynamics[J]. Chinese Quarterly of Mechanics, 2017, 38(2): 23-40.(in Chinese) doi: 10.15959/j.cnki.0254-0053.2017.02.002 [12] CHHANG S, SANSOUR C, HJIAJ M, et al. An energy-momentum co-rotational formulation for nonlinear dynamics of planar beams[J]. Computers and Structures, 2017, 187: 50-63. doi: 10.1016/j.compstruc.2017.03.021 [13] CHO H, KIM H, SHIN S. Geometrically nonlinear dynamic formulation for three-dimensional co-rotational solid elements[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 328: 301-320. doi: 10.1016/j.cma.2017.08.037 [14] KANE T R, RYAN R, BANERJEE A K. Dynamics of a cantilever beam attached to a moving base[J]. Journal of Guidance, Control, and Dynamics, 1987, 10(2): 139-151. doi: 10.2514/3.20195 [15] 杨辉, 洪嘉振, 余征跃. 动力刚化问题的实验研究[J]. 力学学报, 2004, 36(1): 118-124 doi: 10.3321/j.issn:0459-1879.2004.01.019YANG Hui, HONG Jiazhen, YU Zhengyue. Experimental investigation on dynamic stiffening phenomenon[J]. Theoretical and Applied Mechanics, 2004, 36(1): 118-124.(in Chinese) doi: 10.3321/j.issn:0459-1879.2004.01.019 [16] SIMO J C. A finite strain beam formulation, the three-dimensional dynamic problem, part Ⅰ[J]. Computer Methods in Applied Mechanics & Engineering, 1985, 49(1): 55-70. [17] SIMO J C, VU-QUOC L. A three-dimensional finite-strain rod model, part Ⅱ: computational aspects[J]. Computer Methods in Applied Mechanics & Engineering, 1986, 58(1): 79-116. [18] ROMERO I. A comparison of finite elements for nonlinear beams: the absolute nodal coordinate and geometrically exact formulations[J]. Multibody System Dynamics, 2008, 20(1): 51-68. doi: 10.1007/s11044-008-9105-7 [19] 吴坛辉, 洪嘉振, 刘铸永. 非线性几何精确梁理论研究综述[J]. 中国科技论文, 2013, 8(11): 1126-1130 doi: 10.3969/j.issn.2095-2783.2013.11.012WU Tanhui, HONG Jiazhen, LIU Zhuyong. Advances of geometrically exact 3D beam theory[J]. China Sciencepaper, 2013, 8(11): 1126-1130.(in Chinese) doi: 10.3969/j.issn.2095-2783.2013.11.012 [20] 吕品, 廖明夫, 徐阳, 等. 基于几何精确梁理论的风力机叶片单元[J]. 太阳能学报, 2015, 36(10): 2422-2428 doi: 10.3969/j.issn.0254-0096.2015.10.017LÜ Pin, LIAO Mingfu, XU Yang, et al. Beam finite element for wind turbine blade based on geometrically exact beam theory[J]. Acta Energlae Solaris Sinica, 2015, 36(10): 2422-2428.(in Chinese) doi: 10.3969/j.issn.0254-0096.2015.10.017 [21] ROMERO I, ARMERO F. An objective finite element approximation of the kinematics of geometrically exact rods and its use in the formulation of an energy-momentum scheme in dynamics[J]. International Journal for Numerical Methods in Engineering, 2002, 54(12): 1683-1716. doi: 10.1002/nme.486 [22] CRISFIELD M A, JELENIC G. Objectivity of strain measures in the geometrically exact three-dimensional beam theory and its finite-element implementation[J]. Proceedings Mathematical Physical & Engineering Sciences, 1999, 455(1983): 1125-1147. [23] ZUPAN D, SAJE M. The three-dimensional beam theory: finite element formulation based on curvature[J]. Computers & Structures, 2003, 81(18/19): 1875-1888. [24] ZUPAN D, SAJE M. The linearized three-dimensional beam theory of naturally curved and twisted beams: the strain vectors formulation[J]. Computer Methods in Applied Mechanics & Engineering, 2006, 195(33/36): 4557-4578. [25] ČEŠAREK P, SAJE M, ZUPAN D. Dynamics of flexible beams: finite-element formulation based on interpolation of strain measures[J]. Finite Elements in Analysis & Design, 2013, 72: 47-63. [26] 田强, 张云清, 陈立平, 等. 柔性多体系统动力学绝对节点坐标方法研究进展[J]. 力学进展, 2010, 40(2): 189-202 doi: 10.6052/1000-0992-2010-2-J2009-024TIAN Qiang, ZHANG Yunqing, CHEN Liping. et al. Advances in the absolute nodal coordinate method for the flexible multibody dynamics[J]. Advances in Mechanics, 2010, 40(2): 189-202.(in Chinese) doi: 10.6052/1000-0992-2010-2-J2009-024 [27] 田强, 刘铖, 李培, 等. 多柔体系统动力学研究进展与挑战[J]. 动力学与控制学报, 2017, 15(5): 385-405 doi: 10.6052/1672-6553-2017-039TIAN Qiang, LIU Cheng, LI Pei, et al. Advances and challenges in dynamics of flexible multibody systems[J]. Journal of Dynamics and Control, 2017, 15(5): 385-405.(in Chinese) doi: 10.6052/1672-6553-2017-039 [28] HAN Ling, LIU Ying, YANG Bin, et al. Dynamic modeling and simulation of flexible beam finite rotation with ANCF method and FFR method[J]. Mechanika, 2018, 24(5): 715-724. [29] GERSTMAYR J, SUGIYAMA H, MIKKOLA A. Review on the absolute nodal coordinate formulation for large deformation analysis of multibody systems[J]. Journal of Computational and Nonlinear Dynamics, 2013, 8(3): 031016. doi: 10.1115/1.4023487 [30] LI L, CHEN Y Z, ZHANG D G, et al. Large deformation and vibration analysis of microbeams by absolute nodal coordinate formulation[J]. International Journal of Structural Stability and Dynamics, 2019, 19(4): 1950049. doi: 10.1142/S0219455419500494 [31] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003.WANG Xucheng. Finite Element Method[M]. Beijing: Tsinghua Press, 2003. (in Chinese) [32] 齐朝晖, 曹艳, 王刚. 多柔体系统数值分析的模型降噪方法[J]. 力学学报, 2018, 50(4): 863-870 doi: 10.6052/0459-1879-18-111QI Zhaohui, CAO Yan, WANG Gang. Model smoothing methods in numerical analysis of flexible multibody systems[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(4): 863-870.(in Chinese) doi: 10.6052/0459-1879-18-111 [33] 许晶, 李世尧, 王斌泰, 等. 解析型Timoshenko梁有限单元[J]. 西南交通大学学报, 2019, 54(3): 492-498 doi: 10.3969/j.issn.0258-2724.20180176XU Jing, LI Shiyao, WANG Bintai, et al. Analytical finite element for Timoshenko beams[J]. Journal of Southwest Jiaotong University, 2019, 54(3): 492-498.(in Chinese) doi: 10.3969/j.issn.0258-2724.20180176 [34] 周厚德. 岩土工程中条状和板状结构的有限元分析研究[D]. 硕士学位论文. 北京: 清华大学, 2007.ZHOU Houde. Study on strip and slab structures in geotechnical engineering by FEM[D]. Master Thesis. Beijing: Tsinghua University, 2007. (in Chinese) [35] LE T N, BATTINI J M, HJIAJ M. Dynamics of 3D beam elements in a corotational context: a comparative study of established and new formulations[J]. Finite Elements in Analysis and Design, 2012, 61: 97-111. doi: 10.1016/j.finel.2012.06.007 [36] MÄKINEN J. Total Lagrangian Reissner’s geometrically exact beam element without singularities[J]. International Journal for Numerical Methods in Engineering, 2010, 70(9): 1009-1048. -
计量
- 文章访问数: 795
- HTML全文浏览量: 406
- PDF下载量: 87
- 被引次数: 0
渝公网安备50010802005915号