The GMRES(m) Method for Numerical Conformal Mapping of Bounded Multi-Connected Domains
-
摘要:
求解复杂多连通区域的保角变换函数是困难的。针对这一问题，该文将求解保角变换函数转化为利用模拟电荷法求解一对定义在问题区域上的共轭调和函数，再根据边界条件建立约束方程，并利用GMRES(m) (the generalized minimal residual method)算法求解约束方程，获得了模拟电荷，进而构造了高精度的近似保角变换函数，将有界多连通区域映射为三种无界正则狭缝域。数值实验验证了该文算法的有效性。
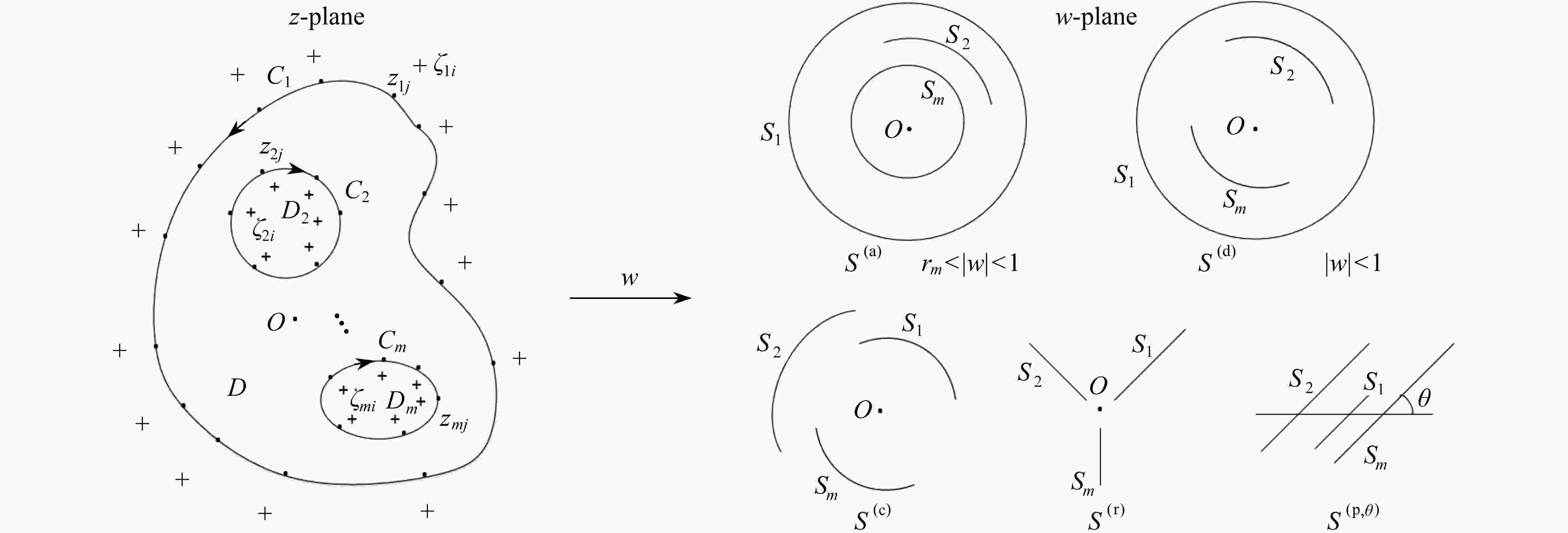
Abstract:It is difficult to solve conformal mapping functions for complex multi-connected domains. In order to overcome this difficulty, the problem of solving conformal mapping functions was transformed into using the charge simulation method to solve a pair of conjugate harmonic functions in the problem domain. The conjugate harmonic functions should satisfy given boundary conditions, which construct a system of linear equations. Then the simulation charges can be computed by means of the GMRES(m) (the generalized minimal residual method) algorithm to solve the linear systems. The approximate conformal mapping functions were constructed accurately to map the bounded multi-connected domain onto 3 unbounded canonical slit domains. Numerical results show that the presented method is effective.
-
图 1 基于模拟电荷法的有界多连通区域保角变换(“·”代表约束点， “+” 代表模拟电荷点)
Figure 1. The conformal mapping of bounded multi-connected regions based on the charge simulation method (“·” represents collocation points, “+” represents charge points)
图 2 模拟电荷点
$ {\zeta _{li}} $ 和约束点$ {z_{kj}} $ 的分布$ ({N_1} = 64,{N_2} = 32,{N_3} = 32) $ Figure 2. The distribution of charge points
$ {\zeta _{li}} $ and collocation points$ {z_{kj}} $ , with$ {N_1} = 64,{N_2} = 32,{N_3} = 32 $ 
图 3 边界保角变换为圆弧狭缝、径向狭缝和平行狭缝
$ (u = 0,v = - 0.1 - 0.1{\rm{i}},\theta = {\text{π}} /4) $ Figure 3. Results of boundaries conformally mapped onto circular slits, radial slits and parallel slits, with
$ u = 0,v = - 0.1 - 0.1{\rm{i}},\theta = {\text{π}} /4 $ 
图 4 对应图3映射到三种狭缝的数值保角变换误差，此时
$ ({N_1} = {N_2} = {N_3} = n) $ Figure 4. Numerical conformal mapping errors corresponding to the mappings onto 3 kinds of slits in fig. 3, with
$ {N_1} = {N_2} = {N_3} = n $ 
图 5 对应图3映射到三种狭缝的数值保角变换误差
$ ({N_1} = 2{N_2} = 2{N_3} = 2n) $ Figure 5. Numerical conformal mapping errors corresponding to the mappings onto 3 kinds of slits in fig. 3, with
$ {N_1} = 2{N_2} = 2{N_3} = 2n $ 
图 9 区域D映射到平行狭缝域的像
$ (\theta = {\text{π}} /4) $ Figure 9. The image of domain D with parallel slits, where
$ \theta = {\text{π}} /4 $ 算法1 模拟电荷的算法 1 输入：$ {\boldsymbol{A}},{\boldsymbol{b}},{{\boldsymbol{x}}_0},\varepsilon $ 2 计算$ {{\boldsymbol{r}}_0} = {\boldsymbol{b}} - {\boldsymbol{A}}{{\boldsymbol{x}}_0},{{\boldsymbol{v}}_1} = \dfrac{{{{\boldsymbol{r}}_0}}}{{\| {{{\boldsymbol{r}}_0}} \|}} $ 3 ${\rm{while}} \quad \delta_{\rm{error}} = {\rm{norm}}({\boldsymbol{r}}) \gt \varepsilon \quad {\rm{do}}$ 4 ${\rm{for}}\;\;\; j = 1:m$ 5 $ {h_{ij}} = {\boldsymbol{v}}_i^{\rm{T}}{\boldsymbol{A}}{{\boldsymbol{v}}_j},i = 1,2,\cdots ,j; $ 6 $ \begin{gathered} {\hat {\boldsymbol{v}} _{j + 1}} = {\boldsymbol{A}}{{\boldsymbol{v}}_j} - \sum\nolimits_{i = 1}^j {{h_{ij}}{{\boldsymbol{v}}_i}} ; \\\end{gathered} $ 7 $ {h_{j + 1,j}} = \| {{{\hat {\boldsymbol{v}} }_{j + 1}}} \|; $ 8 $ {{\boldsymbol{v}}_{j + 1}} = {\hat {\boldsymbol{v}} _{j + 1}}/{h_{j + 1,j}}; $ 9 $ {\rm{end}}\quad {\rm{for}} $ 10 ${\bar {\boldsymbol{H}}_m} = ({h_{ij}}),{{\boldsymbol{V}}_m} = ({{\boldsymbol{v}}_i}),$计算${{\boldsymbol{y}}_m} ,$ 11 ${\rm{ if}} \quad \| {\| {{{\boldsymbol{r}}_0}} \|{e_1} - {{\bar {\boldsymbol{H}}}_m}{{\boldsymbol{y}}_m}} \| = \min ; $ 令$ {{\boldsymbol{x}}_m} = {{\boldsymbol{x}}_0} + {{\boldsymbol{V}}_m}{{\boldsymbol{y}}_m}; $ $ {\rm{end}}\quad {\rm{if}} $ 12 $ {\boldsymbol{r}} = {\boldsymbol{b}} - {\boldsymbol{A}}{{\boldsymbol{x}}_m}; $ 13 $ {\rm{end}}\quad {\rm{while}} $ 14 输出：$ {{\boldsymbol{x}}_m} $ 
下载: 导出CSV
-
[1] LYU Y Y, JIANG J, WANG Y L, et al. Superconducting diode effect via conformal-mapped nanoholes[J]. Nature Communications, 2021, 12: 2703. doi: 10.1038/s41467-021-23077-0 [2] 朱满座. 数值保角变换及其在电磁理论中的应用[D]. 博士学位论文. 西安: 西安电子科技大学, 2008.ZHU Manzuo. Numerical conformal mapping and its applications in the electromagnetic theory[D]. PhD Thesis. Xi’an: Xidian University, 2008. (in Chinese) [3] 曹伟杰. 保形变换理论及其应用[M]. 上海: 上海科学技术文献出版社, 1988.CAO Weijie. Conformal Mapping Theory and Its Application[M]. Shanghai: Shanghai Scientific and Technical Literature Press, 1988. (in Chinese) [4] CONSTANTIN A, STRAUSS W, VARVARUCA E. Global bifurcation of steady gravity water waves with critical layers[J]. Acta Mathematica, 2016, 217: 195-262. doi: 10.1007/s11511-017-0144-x [5] SUNAO M, WOOYOUNG C. A numerical study on parasitic capillary waves using unsteady conformal mapping[J]. Journal of Computational Physics, 2017, 328: 234-257. doi: 10.1016/j.jcp.2016.10.015 [6] 郑志强. 单位圆到任意曲线保角变换的近似计算方法[J]. 应用数学和力学, 1992, 13(5): 449-457ZHENG Zhiqiang. An approximate method on the conformal mapping from a unit circle to an arbitrary curve[J]. Applied Mathematics and Mechanics, 1992, 13(5): 449-457.(in Chinese) [7] SANGAWI A W K, MURID A H M, NASSER M M S. Annulus with circular slit map of bounded multiply connected regions via integral equation method[J]. Bulletin of the Malaysian Mathematical Society, 2012, 4(4): 945-959. [8] KOKKINOS C A, PAPAMICHAEL N, SIDERIDIS A B. An orthonormalization method for the approximate conformal mapping of multiply-connected domains[J]. IMA Journal of Numerical Analysis, 1990, 10(3): 343-359. doi: 10.1093/imanum/10.3.343 [9] TREFETHEN L N. Numerical conformal mapping with rational functions[J]. Computational Methods and Function Theory, 2020, 20: 369-387. doi: 10.1007/s40315-020-00325-w [10] LO W L, WU N J, CHEN C S, et al. Exact boundary derivative formulation for numerical conformal mapping method[J]. Mathematical Problems in Engineering, 2016, 2: 1-18. [11] AMANO K. Numerical conformal mapping of exterior domains based on the charge simulation method[J]. Information Processing Society of Japan Journal, 1988, 29(1): 62-72. [12] AMANO K. A charge simulation method for the numerical conformal mapping of interior, exterior and doubly-connected domains[J]. Journal of Computational and Applied Mathematics, 1994, 53: 353-370. doi: 10.1016/0377-0427(94)90063-9 [13] NEHARI Z. Conformal Mapping[M]. New York: Dover Publications, 1952. [14] OKANO D, OGATA H, AMANO K, et al. Numerical conformal mappings of bounded multiply connected domains by the charge simulation method[J]. Journal of Computational and Applied Mathematics, 2003, 159(1): 109-117. doi: 10.1016/S0377-0427(03)00572-7 [15] 吕毅斌, 赖富明, 王樱子, 等. 基于GMRES(m)法的双连通区域数值保角变换的计算法[J]. 数学杂志, 2016, 36(5): 1028-1034 doi: 10.3969/j.issn.0255-7797.2016.05.017LÜ Yibin, LAI Fuming, WANG Yingzi, et al. The GMRES(m) method for numerical conformal mapping of doubly-connected domain[J]. Journal of Mathematics, 2016, 36(5): 1028-1034.(in Chinese) doi: 10.3969/j.issn.0255-7797.2016.05.017 [16] MUROTA K. Comparison of conventional and “invariant” schemes of fundamental solutions method for annular domains[J]. Japan Journal of Industrial and Applied Mathematics, 1995, 12(1): 61-85. doi: 10.1007/BF03167382 [17] SAAD Y, SCHULTZ M H. GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems[J]. SIAM Journal on Scientific and Statistical Computing, 1986, 7(3): 856-869. doi: 10.1137/0907058 -
计量
- 文章访问数: 887
- HTML全文浏览量: 317
- PDF下载量: 74
- 被引次数: 0
渝公网安备50010802005915号