Vibration and Buckling Characteristics of 2D Functionally Graded Microbeams With Variable Cross Sections
-
摘要:
基于修正的偶应力理论和Timoshenko梁理论，应用变分原理建立了变截面二维功能梯度微梁的自由振动和屈曲力学模型。模型中包含金属组分和陶瓷组分的材料内禀特征尺度参数，可以预测微梁力学行为的尺度效应。采用Ritz法给出了任意边界条件下微梁振动频率和临界屈曲载荷的数值解。数值算例表明：微梁厚度减小时，无量纲一阶频率和无量纲临界屈曲载荷增大，尺度效应增强。锥度比对微梁一阶频率的影响与边界条件密切相关，同时，对应厚度和对应宽度锥度比的影响也有明显差异。变截面微尺度梁无量纲一阶频率随着陶瓷和金属的材料内禀特征尺度参数比的增加而增大，且不同边界条件时增大程度不同。厚度方向和轴向功能梯度指数对微梁的一阶频率和屈曲载荷也有显著的影响。
Abstract:Based on the modified couple stress theory and the Timoshenko beam theory, the free vibration and buckling mechanics model for 2D functionally graded microbeams with variable cross sections was established by means of the variational principle. The model contains the intrinsic material length scale parameters of the metal and ceramic components, which can predict the size effects of microbeams. The Ritz method was used to obtain the numerical solution of the vibration frequencies and critical buckling loads of the microbeams under arbitrary boundary conditions. Numerical examples reveal that, when the thickness of the microbeam decreases, the dimensionless 1st-order frequency and the dimensionless critical buckling load will increase, and the scale effect will grow larger. The effect of the taper ratio on the dimensionless 1st-order frequency of the microbeam is closely related to the boundary conditions. At the same time, the effects of the taper ratios of the thickness and the width are also significantly different. The dimensionless 1st-order frequencies of microbeams increase with the material length scale parameter ratios of ceramic and metal, and the degrees of increase are different under different boundary conditions. The thick-direction and axial material gradient indexes also have significant influences on the free vibration and buckling behavior of the microbeam.
-
图 1 二维变截面功能梯度微梁示意图
Figure 1. Schematic diagram of a 2D variable-cross-section functionally graded microbeam
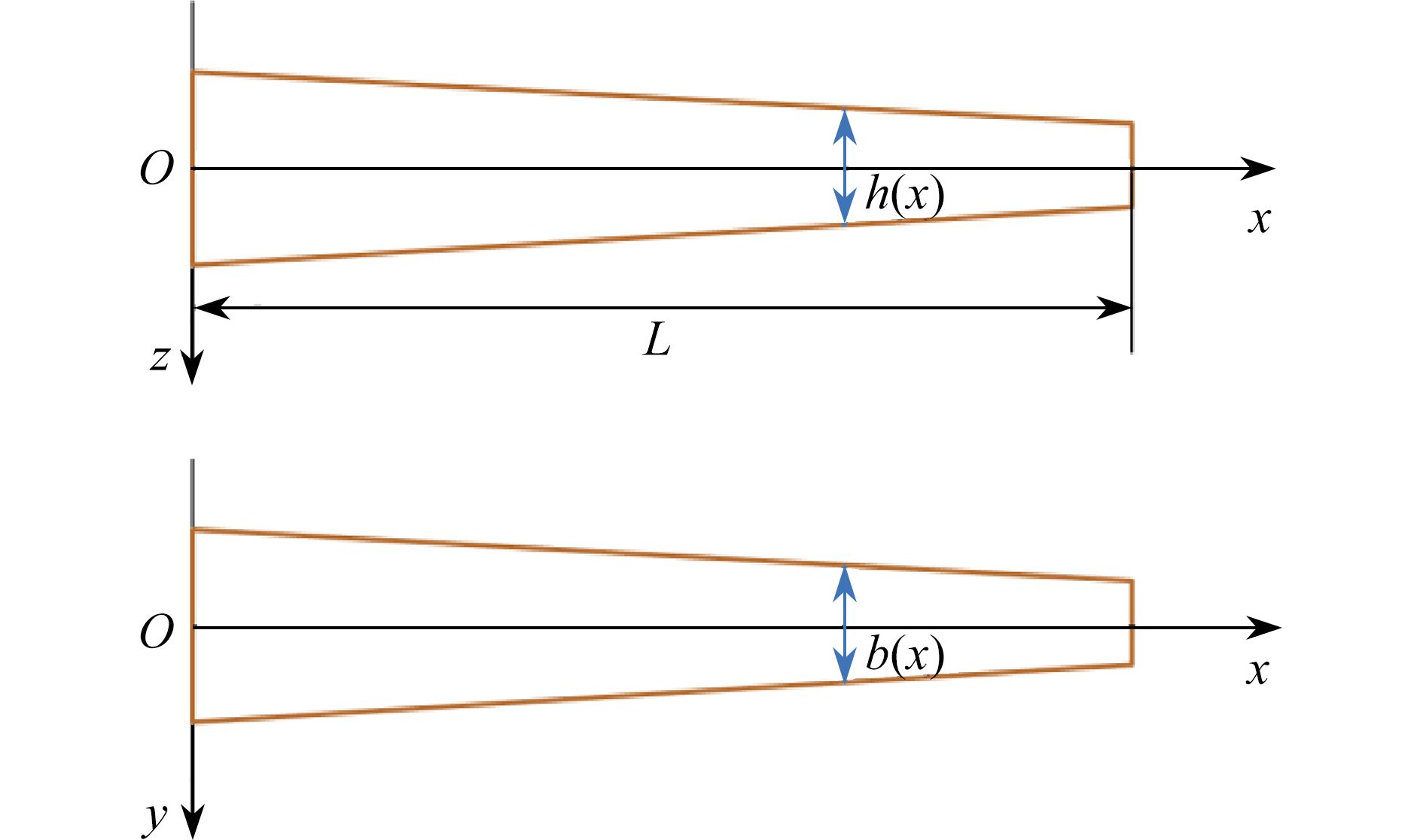
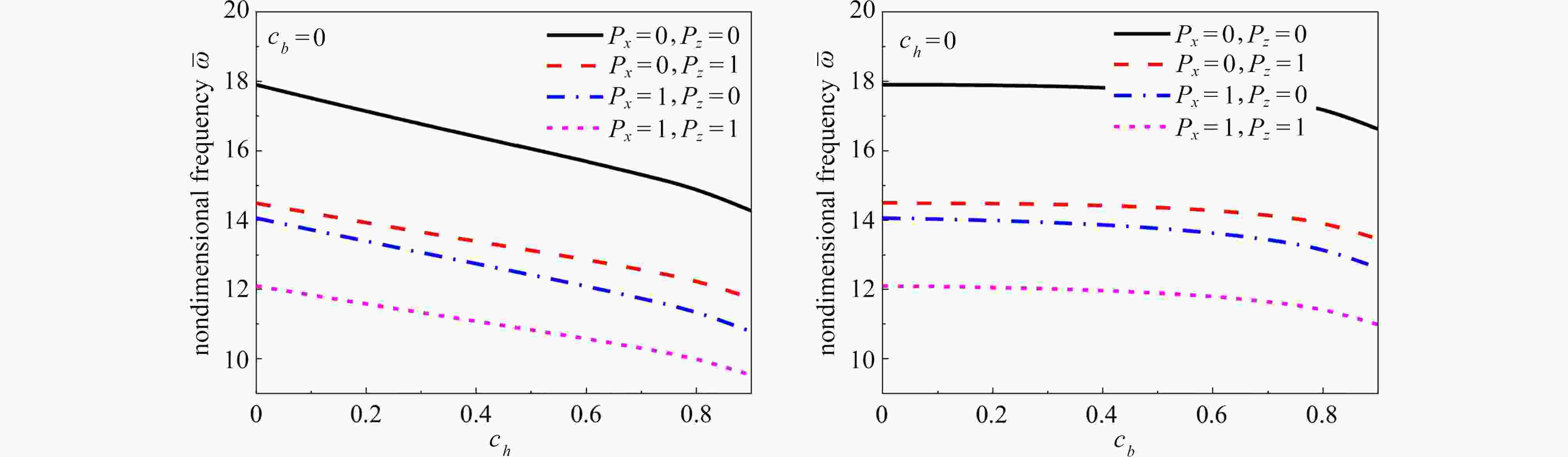
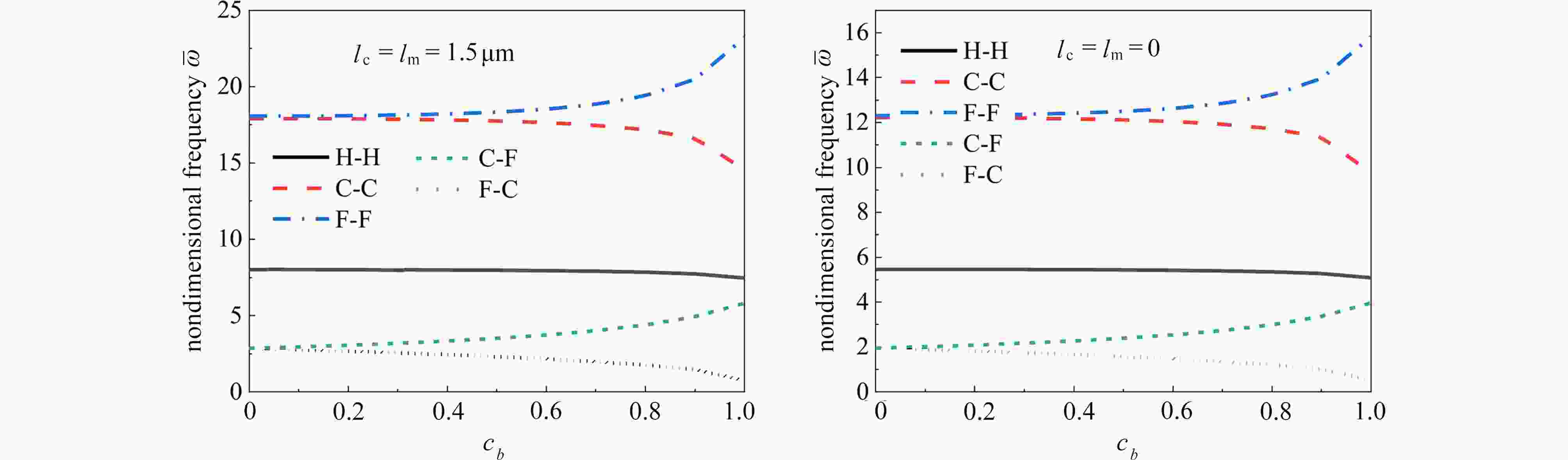
图 2 两端固支边界时锥度比对微梁无量纲频率的影响（
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${l_{\rm{c}}} = {l_{\rm{m}}} = 1.5{\text{ μm}}$ ）Figure 2. The effects of taper ratios on the dimensionless frequencies of microbeams with clamped boundary conditions (
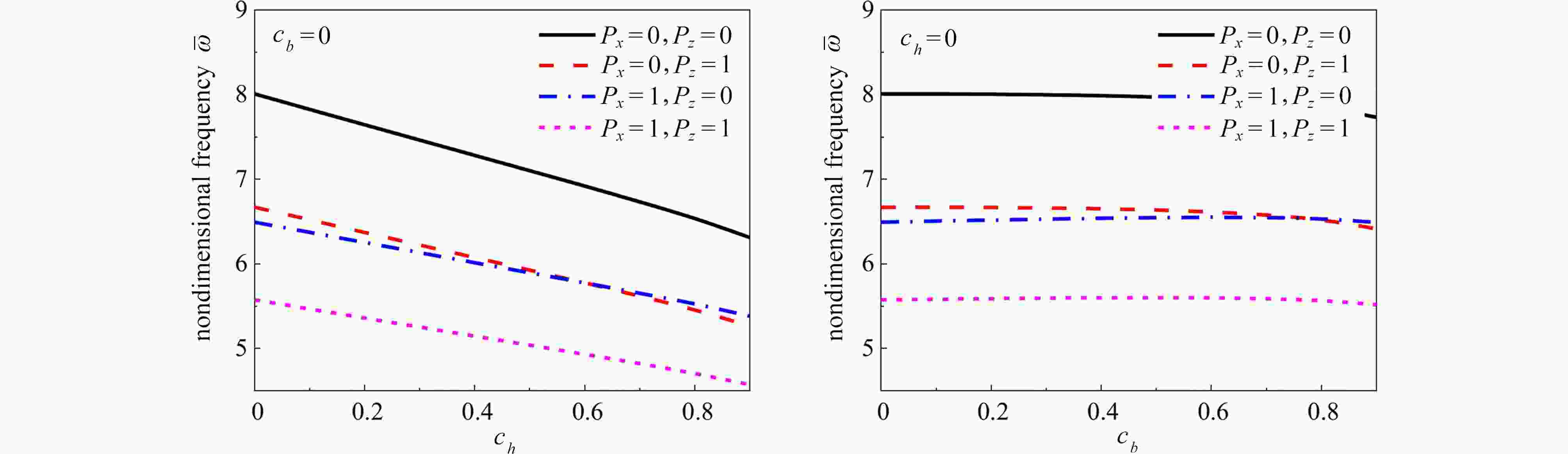
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${l_{\rm{c}}} = {l_{\rm{m}}} = 1.5{\text{ μm}}$ )
图 3 两端铰支边界时锥度比对微梁无量纲频率的影响（
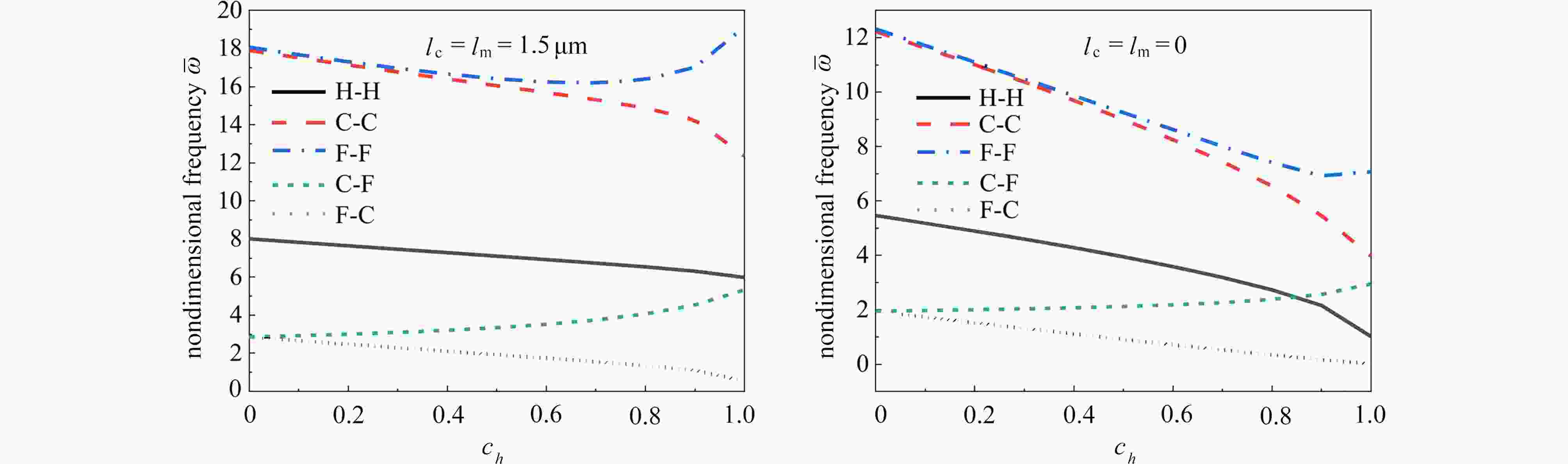
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${l_{\rm{c}}} = {l_{\rm{m}}} = 1.5{\text{ μm}}$ ）Figure 3. The effects of taper ratios on the dimensionless frequencies of microbeams with hinged boundary conditions (
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${l_{\rm{c}}} = {l_{\rm{m}}} = 1.5{\text{ μm}}$ )
图 4 两端自由边界时锥度比对微梁无量纲频率的影响（
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${l_{\rm{c}}} = {l_{\rm{m}}} = 1.5{\text{ μm}}$ ）Figure 4. The effects of taper ratios on the dimensionless frequencies of microbeams with free boundary conditions （
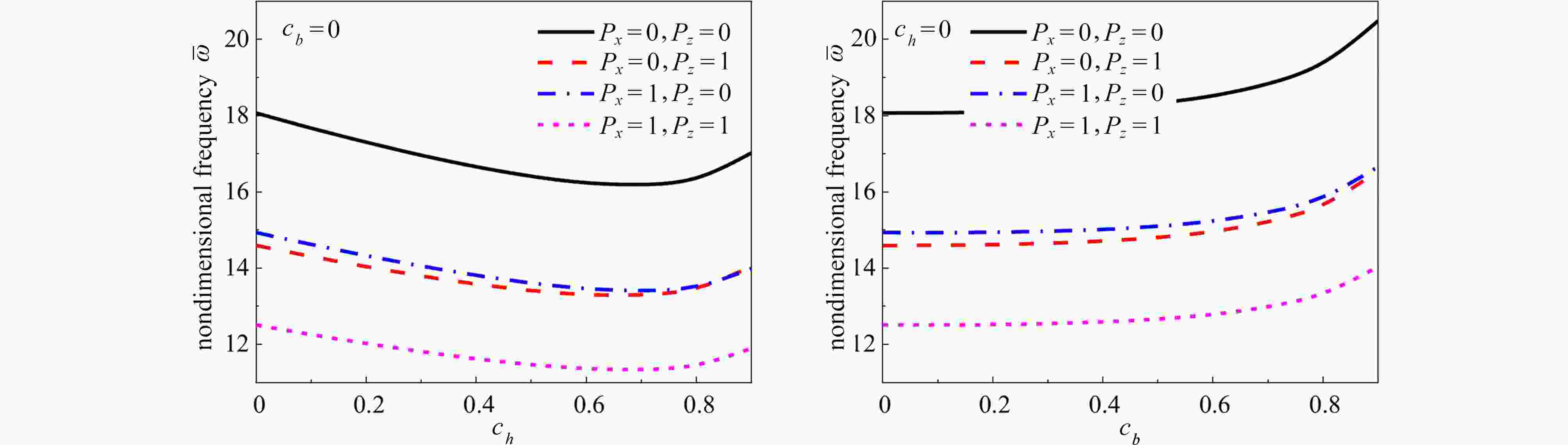
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${l_{\rm{c}}} = {l_{\rm{m}}} = 1.5{\text{ μm}}$ ）
图 5 悬臂边界时锥度比对微梁无量纲频率的影响（
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${l_{\rm{c}}} = {l_{\rm{m}}} = 1.5{\text{ μm}}$ ）Figure 5. The effects of taper ratios on the dimensionless frequencies of microbeams with cantilever boundary conditions (
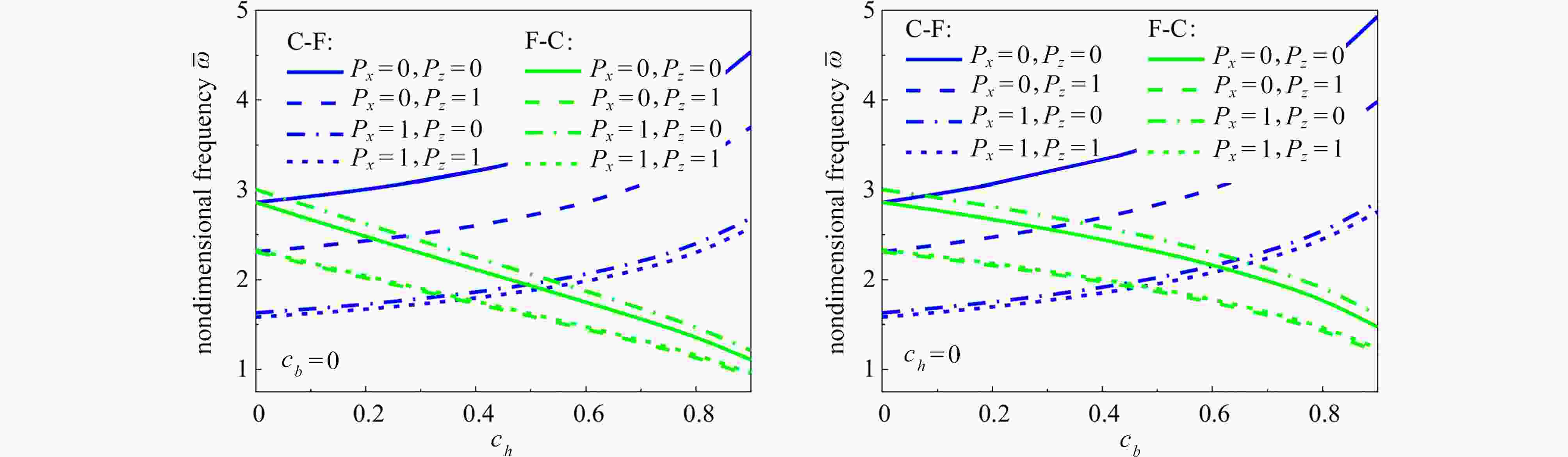
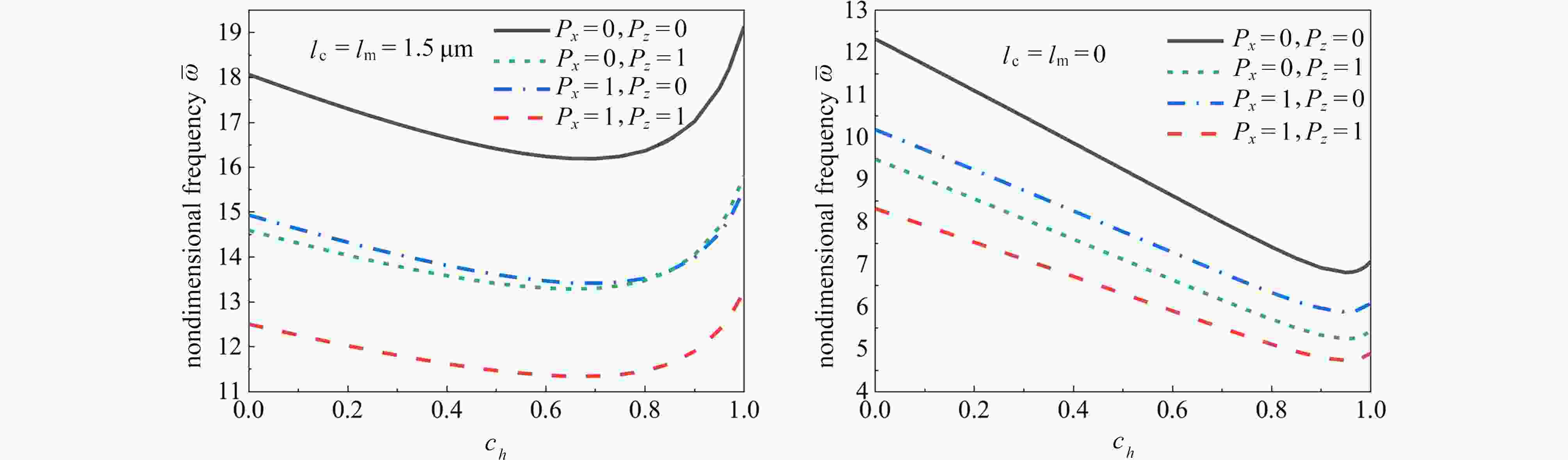
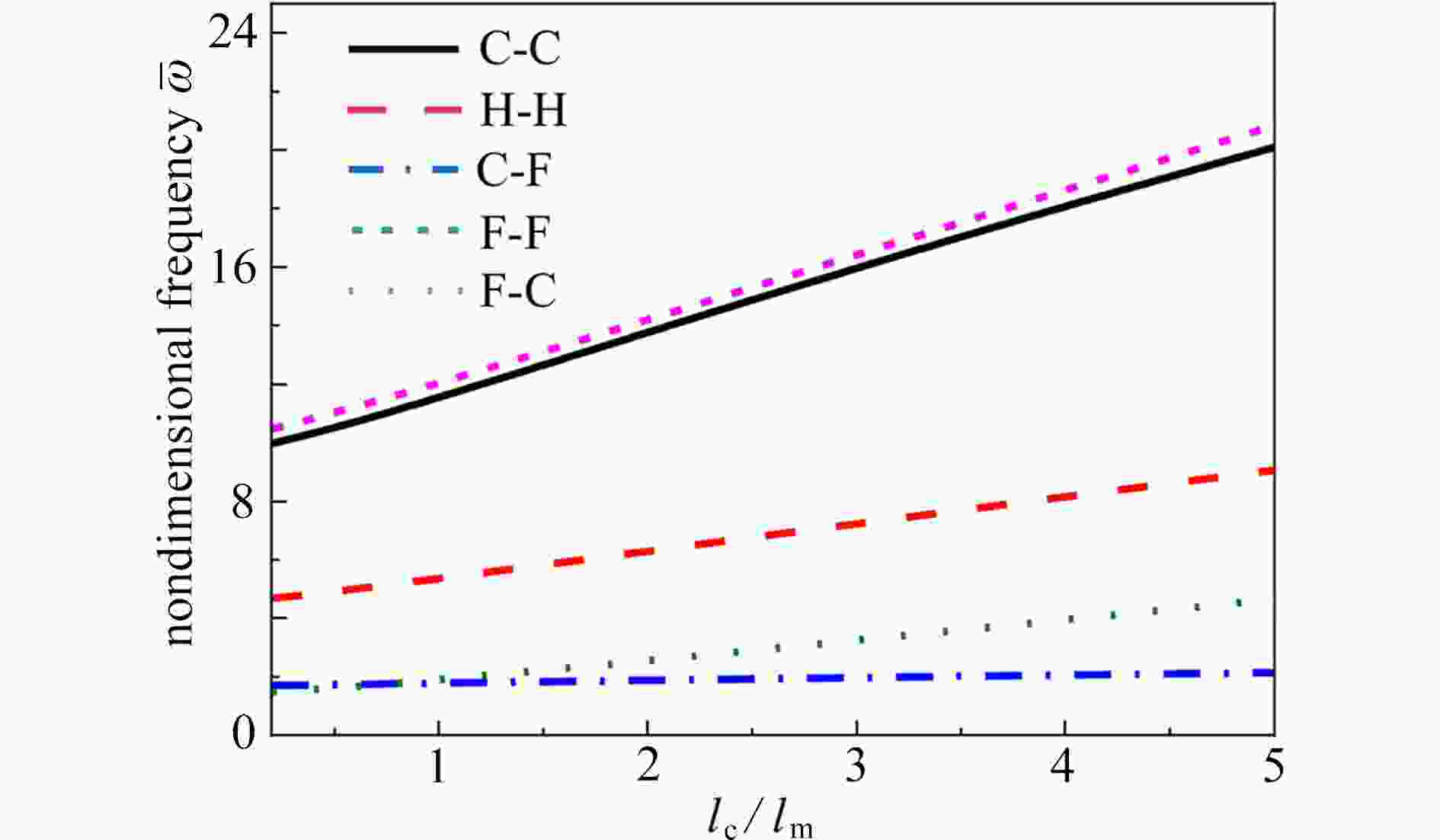
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${l_{\rm{c}}} = {l_{\rm{m}}} = 1.5{\text{ μm}}$ )
图 6 轴向功能梯度指数对微梁无量纲频率的影响（
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${c_h} = {c_b} = 0$ ，$P_z = 0$ ）Figure 6. The effects of axial functional gradient indexes on the dimensional frequencies of microbeams （
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${c_h} = {c_b} = 0$ ，$P_z = 0$ ）
图 7 锥度比（ch）对微梁无量纲频率的影响（
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${c_b} = 0$ ，$P_x = P_z = 0$ ）Figure 7. The effects of taper ratios（ch） on the dimensional frequencies of microbeams （
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${c_b} = 0$ ，$P_x = P_z = 0$ ）
图 8 锥度比（cb）对微梁无量纲频率的影响（
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${c_h} = 0$ ，$P_x = P_z = 0$ ）Figure 8. The effects of taper ratios（cb）on the dimensional frequencies of microbeams （
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${c_h} = 0$ ，$P_x = P_z = 0$ ）
图 9 锥度比（ch）对自由边界条件微梁无量纲频率的影响（
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${c_b} = 0$ ，F-F）Figure 9. The effects of taper ratios（ch） on the dimensional frequencies of microbeams with free boundary conditions （
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${c_b} = 0$ ，F-F）
图 10 长厚比对微梁无量纲频率的影响（C-C，
${c_h} = {c_b} = 0.2$ ，$P_x = $ $ P_z = 1$ ，${l_c} = {l_m} = 1.5{\text{ μm}}$ ）Figure 10. The effects of length-to-thickness ratios on the dimensionless frequencies of microbeams (C-C,
${c_h} = {c_b} = 0.2$ ,$P_x = P_z = 1$ ,${l_{\rm{c}}} = {l_{\rm{m}}} = 1.5{\text{ μm}}$ )
图 11 陶瓷和金属的材料尺度参数比对微梁无量纲频率的影响（
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，$P_x = P_z = 1$ ，${c_h} = {c_b} = 0.2$ ，${l_{\rm{m}}} = 1.5{\text{ μm}}$ ）Figure 11. The effects of the length scale parameter ratios of ceramic and metal on the dimensionless frequencies of microbeams (
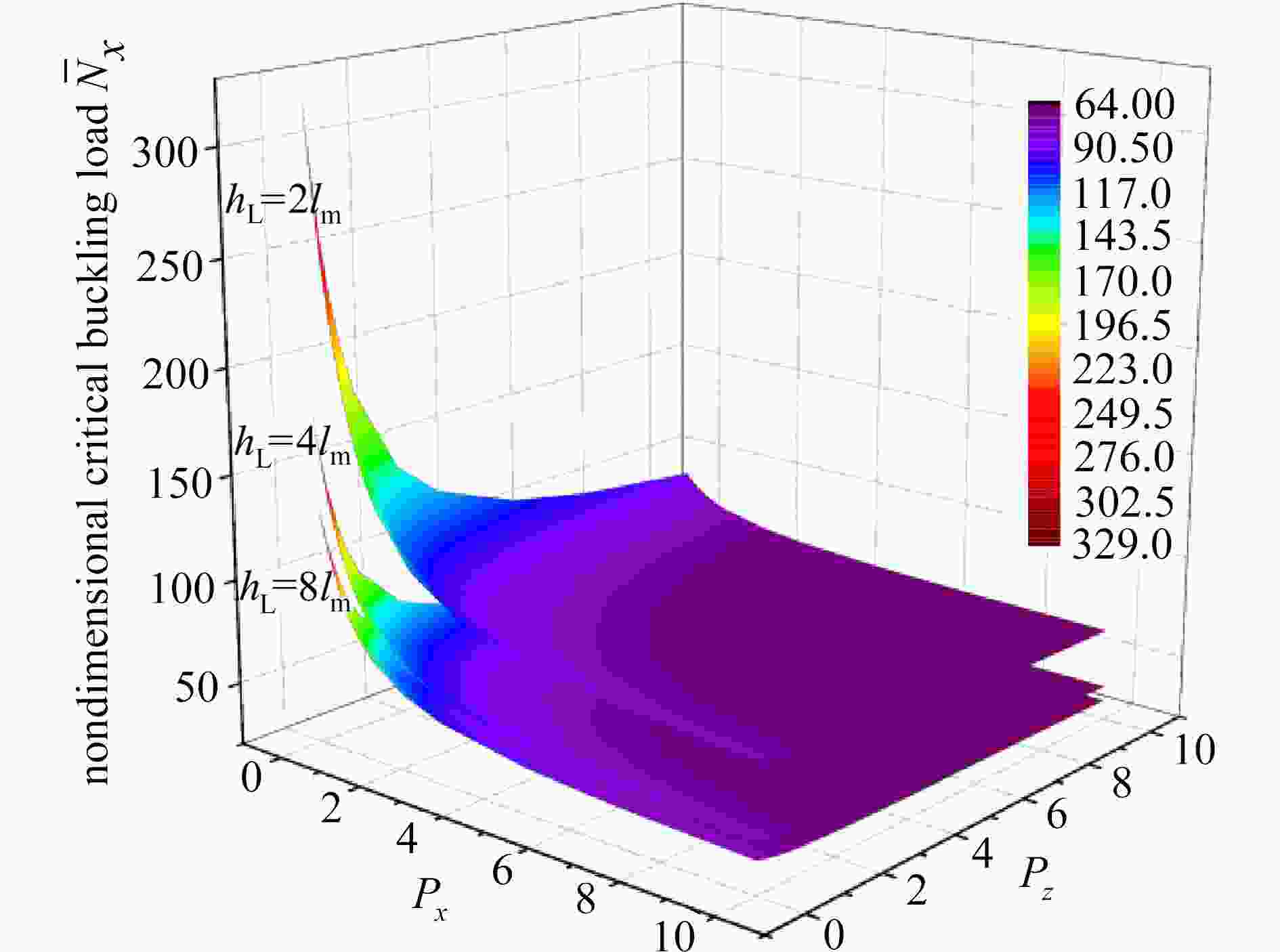
${h_{\rm{L}}} = 3{\text{ μm}}$ ，$L = 20{h_{\rm{L}}}$ ，$P_x = P_z = 1$ ，${c_h} = {c_b} = 0.2$ ，${l_{\rm{m}}} = 1.5{\text{ μm}}$ )
图 12 两端固支（C-C）微梁的临界屈曲载荷随功能梯度指数和轴向功能梯度指数的变化情况（
$L = 20{h_{\rm{L}}}$ ，${l_{\rm{c}}} = {l_{\rm{m}}} = 1.5{\text{ μm}}$ ，${c_h} = {c_b} = 0.2$ ）Figure 12. The effects of the functionally graded indexes on the critical buckling loads of microbeams （
$L = 20{h_{\rm{L}}}$ ，${l_{\rm{c}}} = {l_{\rm{m}}} = 1.5{\text{ μm}}$ ，${c_h} = {c_b} = 0.2$ ）表 1 不同边界条件时p1, p2, s1, s2及t1, t2的取值
Table 1. Values of p1，p2，s1，s2 and t1，t2 with different boundary conditions
p1 p2 s1 s2 t1 t2 C-C 1 1 2 2 1 1 H-H 1 1 1 1 0 0 F-F 0 0 0 0 0 0 C-H 1 1 2 1 1 0 H-C 1 1 1 2 0 1 C-F 1 0 2 0 1 0 F-C 0 1 0 2 0 1 
下载: 导出CSV
表 2 二维功能梯度等截面微梁无量纲频率的收敛性分析（
${h_{\rm{L}}} = 1.5\;{\text{μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${c_h} = {c_b} = 0$ ，${l_{\rm{c}}} = {l_{\rm{m}}} = 1.5\;{\text{μm}}$ ）Table 2. Convergence analysis of dimensionless frequencies of the 2D functionally graded equal-cross-section microbeam（
${h_{\rm{L}}} = 1.5\;{\text{μm}}$ ，$L = 20{h_{\rm{L}}}$ ，${c_h} = {c_b} = 0$ ，${l_{\rm{c}}} = {l_{\rm{m}}} = {\text{1.5}}\;{\text{μ}} {\rm{m}}$ ）${n_{\rm{t}}}$ $P_x = P_z = 0$ $P_x = 0,\; P_z = 1$ $P_x = 1,\;P_z = 0$ $P_x = P_z = 1$ 6 28.5940 23.6911 22.4498 19.5610 8 28.5838 23.6829 22.4363 19.5521 10 28.5799 23.6795 22.4307 19.5484 12 28.5785 23.6783 22.4286 19.5471 14 28.5781 23.6779 22.4279 19.5466 16 28.5780 23.6778 22.4277 19.5465 18 28.5779 23.6777 22.4276 19.5464
下载: 导出CSV
表 3 基于本文模型的宏观功能梯度等截面梁无量纲频率与文献[34]中结果的对比（
$h = 1{\text{ m}}$ ）Table 3. Comparison of dimensionless frequencies of macro traditional equal-cross-section FG beams with ref.[34] (
$h = 1{\text{ m}}$ )BC L/h model Pz 0 1 2 5 10 C-F 5 present 1.89472 1.46296 1.33372 1.26441 1.22393 ref. [34] 1.89479 1.46300 1.33376 1.26445 1.22398 20 present 1.94957 1.50104 1.36968 1.30374 1.26494 ref. [34] 1.94957 1.50104 1.36968 1.30375 1.26495 C-C 5 present 10.0198 7.91520 7.20210 6.65777 6.33031 ref. [34] 10.0344 7.92529 7.21134 6.66764 6.34062 20 present 12.2226 9.43080 8.60350 8.16921 7.91202 ref. [34] 12.2235 9.43135 8.60401 8.16985 7.91275
下载: 导出CSV
表 4 基于本文模型的宏观均质锥形梁前三阶无量纲频率与文献[35]中结果的对比（C-F边界，
$ P_z =P_x =0 $ ，此算例中$\tilde \omega {\text{ = }}\omega {L^2}\sqrt {{{{\rho _{\rm{c}}}{A_{\rm{L}}}}/ ({{E_{\rm{c}}}{I_{\rm{L}}}})}} $ ，${A_{\rm{L}}} = {h_{\rm{L}}}{b_{\rm{L}}}$ ，${I_{\rm{L}}} = {{{b_{\rm{L}}}{h_{\rm{L}}}^3}/{12}}$ ）Table 4. Comparison of the 1st 3 order dimensionless frequencies of macro traditional tapered beams with ref.[35] (in this case：C-F boundary condition，
$ P_z =P_x =0 $ ，$\tilde \omega {\text{ = }}\omega {L^2}\sqrt {{{{\rho _{\rm{c}}}{A_{\rm{L}}}} /({{E_{\rm{c}}}{I_{\rm{L}}}})}}$ ，${A_{\rm{L}}} = {h_{\rm{L}}}{b_{\rm{L}}}$ ，${I_{\rm{L}}} = {{{b_{\rm{L}}}{h_{\rm{L}}}^3}/{12}}$ )cb model ch=0 ch model cb=0 ${\tilde \omega _1}$ ${\tilde \omega _2}$ ${\tilde \omega _3}$ ${\tilde \omega _1}$ ${\tilde \omega _2}$ ${\tilde \omega _3}$ 0 present 3.5090 21.7373 59.7804 0 present 3.5090 21.7373 59.7804 ref. [35] 3.5160 22.0345 61.6972 ref. [35] 3.5160 22.0345 61.6972 0.4 present 4.0879 22.8068 60.8214 0.4 present 3.7307 18.9405 49.3059 ref. [35] 4.0970 23.1186 62.7763 ref. [35] 3.7371 19.1138 50.3537 0.8 present 5.3829 25.2969 63.6608 0.8 present 4.2863 15.6622 36.4756 ref. [35] 5.3976 25.6558 65.7470 ref. [35] 4.2925 15.7427 36.8855
下载: 导出CSV
-
[1] SINA S, NAVAZI H M, HADDADPOUR H. An analytical method for free vibration analysis of functionally graded beams[J]. Materials and Design, 2009, 30(3): 741-747. doi: 10.1016/j.matdes.2008.05.015 [2] ALSHORBAGY A E, ELTAHER M A, MAHMOUD F. Free vibration characteristics of a functionally graded beam by finite element method[J]. Applied Mathematical Modelling, 2011, 35(1): 412-425. doi: 10.1016/j.apm.2010.07.006 [3] ŞIMŞEK M. Vibration analysis of a functionally graded beam under a moving mass by using different beam theories[J]. Composite Structures, 2010, 92(4): 904-917. doi: 10.1016/j.compstruct.2009.09.030 [4] AYDOGDU M. Semi-inverse method for vibration and buckling of axially functionally graded beams[J]. Journal of Reinforced Plastics and Composites, 2008, 27(7): 683-691. doi: 10.1177/0731684407081369 [5] 王伟斌, 杨文秀, 滕兆春. 多孔功能梯度材料Timoshenko梁的自由振动分析[J]. 计算力学学报, 2021, 5: 1-13 doi: 10.7511/jslx20200311001WANG Weibin, YANG Wenxiu, TENG Zhaochun. Free vibration analysis of porous functionally graded materials Timoshenko beam[J]. Chinese Journal of Computational Mechanics, 2021, 5: 1-13.(in Chinese) doi: 10.7511/jslx20200311001 [6] 蒲育, 周凤玺. FGM梁临界屈曲载荷的改进型GDQ法分析[J]. 应用基础与工程科学学报, 2019, 27(6): 1308-1320 doi: 10.16058/j.issn.1005-0930.2019.06.011PU Yu, ZHOU Fengxi. Critical buckling loads analysis of FGM beams by a modified generalized differential quadrature method[J]. Journal of Basic Science Engineering, 2019, 27(6): 1308-1320.(in Chinese) doi: 10.16058/j.issn.1005-0930.2019.06.011 [7] 马连生, 贾金政. 机械载荷作用下功能梯度梁的过屈曲分析[J]. 兰州理工大学学报, 2020, 46(3): 160-164 doi: 10.3969/j.issn.1673-5196.2020.03.029MA Liansheng, JIA Jinzheng. Analysis of mechanical postbuckling behavior of functionally graded beams[J]. Journal of Lanzhou University of Technology, 2020, 46(3): 160-164.(in Chinese) doi: 10.3969/j.issn.1673-5196.2020.03.029 [8] 葛仁余, 张金轮, 韩有民, 等. 功能梯度变截面梁自由振动和稳定性研究[J]. 应用力学学报, 2017, 34(5): 875-880, 1012GE Renyu, ZHANG Jinlun, HAN Youmin, et al. Free vibration and stability of axially functionally graded beams with variable cross-section[J]. Chinese Journal of Applied Mechanics, 2017, 34(5): 875-880, 1012.(in Chinese) [9] 杜运兴, 程鹏, 周芬. 变截面功能梯度Timoshenko梁的自由振动分析[J]. 湖南大学学报(自然科学版), 2021, 48(5): 55-62.DU Yunxing, CHENG Peng, ZHOU Fen. Free vibration analysis of functionally graded Timoshenko beams with variable section[J]. Journal of Hunan University(Natural Sciences), 2021, 48(5): 55-62.(in Chinese) [10] LÜ C, LIM C W, CHEN W. Size-dependent elastic behavior of FGM ultra-thin films based on generalized refined theory[J]. International Journal of Solids and Structures, 2009, 46(5): 1176-1185. doi: 10.1016/j.ijsolstr.2008.10.012 [11] SHAAT M, MAHMOUD F, ALSHORBAGY A E, et al. Finite element analysis of functionally graded nano-scale films[J]. Finite Elements in Analysis and Design, 2013, 74: 41-52. doi: 10.1016/j.finel.2013.05.012 [12] FLECK N A, MULLER G M, ASHBY M F, et al. Strain gradient plasticity: theory and experiment[J]. Acta Metallurgica et Materialia, 1994, 42(2): 475-487. doi: 10.1016/0956-7151(94)90502-9 [13] LAM D C C, MULLER G M, ASHBY M F, et al. Experiments and theory in strain gradient elasticity[J]. Journal of the Mechanics and Physics of Solids, 2003, 51(8): 1477-1508. doi: 10.1016/S0022-5096(03)00053-X [14] LEI J, HE Y, GUO S, et al. Size-dependent vibration of nickel cantilever microbeams: experiment and gradient elasticity[J]. AIP Advances, 2016, 6(10): 105202. doi: 10.1063/1.4964660 [15] LI Z, HE Y, GUO S, et al. A standard experimental method for determining the material length scale based on modified couple stress theory[J]. International Journal of Mechanical Sciences, 2018, 141: 198-205. doi: 10.1016/j.ijmecsci.2018.03.035 [16] ERINGEN A C, EDELEN D. On nonlocal elasticity[J]. International Journal of Engineering Science, 1972, 10(3): 233-248. doi: 10.1016/0020-7225(72)90039-0 [17] YANG F, CHONG A C M, LAM D C C, et al. Couple stress based strain gradient theory for elasticity[J]. International Journal of Solids and Structures, 2002, 39(10): 2731-2743. doi: 10.1016/S0020-7683(02)00152-X [18] ASGHARI M, CHONG M C, LAM D C C, et al. On the size-dependent behavior of functionally graded micro-beams[J]. International Journal of Solids and Structure, 2010, 31(5): 2324-2329. [19] REDDY J N. Microstructure-dependent couple stress theories of functionally graded beams[J]. Journal of the Mechanics and Physics of Solids, 2011, 59(11): 2382-2399. doi: 10.1016/j.jmps.2011.06.008 [20] ŞIMŞEK M J, REDDY J N. Bending and vibration of functionally graded microbeams using a new higher order beam theory and the modified couple stress theory[J]. International Journal of Engineering Science, 2013, 64: 37-53. doi: 10.1016/j.ijengsci.2012.12.002 [21] AL-BASYOUNI K S, TOUNSI A, MAHMOUD S R. Size dependent bending and vibration analysis of functionally graded micro beams based on modified couple stress theory and neutral surface position[J]. Composite Structures, 2015, 125: 621-630. doi: 10.1016/j.compstruct.2014.12.070 [22] LEI Jian, HE Yuming, ZHANG Bo, et al. Bending and vibration of functionally graded sinusoidal microbeams based on the strain gradient elasticity theory[J]. International Journal of Engineering Science, 2013, 72: 36-52. doi: 10.1016/j.ijengsci.2013.06.012 [23] LEI J, HE Y, ZHANG B, et al. Thermal buckling and vibration of functionally graded sinusoidal microbeams incorporating nonlinear temperature distribution using DQM[J]. Journal of Thermal Stresses, 2017, 40(6): 665-689. doi: 10.1080/01495739.2016.1258602 [24] LEI J, HR M. Effect of nonlocal thermoelasticity on buckling of axially functionally graded nanobeams[J]. Journal of Thermal Stresses, 2019, 42(4): 526-539. doi: 10.1080/01495739.2018.1536866 [25] 杨子豪, 贺丹. 考虑尺度依赖的平面正交各向异性功能梯度微梁的自由振动分析[J]. 复合材料学报, 2017, 34(10): 2375-2384 doi: 10.13801/j.cnki.fhclxb.20170228.003YANG Zihao, HE Dan. Size-dependent free vibration analysis of plane orthotropic functionally graded micro-beams[J]. Acta Materiae Compositae Sinica, 2017, 34(10): 2375-2384.(in Chinese) doi: 10.13801/j.cnki.fhclxb.20170228.003 [26] EBRAHIMI F, BARATI M R. A nonlocal strain gradient refined beam model for buckling analysis of size-dependent shear-deformable curved FG nanobeams[J]. Composite Structures, 2017, 159: 174-182. doi: 10.1016/j.compstruct.2016.09.058 [27] LEI J, GUO S, HE M, et al. Postbuckling analysis of bi-directional functionally graded imperfect beams based on a novel third-order shear deformation theory[J]. Composite Structures, 2019, 209: 811-829. doi: 10.1016/j.compstruct.2018.10.106 [28] TANG Y, DING Q. Nonlinear vibration analysis of a bi-directional functionally graded beam under hygro-thermal loads[J]. Composite Structures, 2019, 225: 111076. doi: 10.1016/j.compstruct.2019.111076 [29] BARATI A, HADI A, NORROZI R, et al. On vibration of bi-directional functionally graded nanobeams under magnetic field[J]. Mechanics Based Design of Structures and Machines, 2020, 50(2): 468-485. [30] HUANG Y, OUYANG Z Y. Exact solution for bending analysis of two-directional functionally graded Timoshenko beams[J]. Archive of Applied Mechanics, 2020, 90: 1005-1023. doi: 10.1007/s00419-019-01655-5 [31] WATTANASAKULPONG N, UNGBHAKORN V. Linear and nonlinear vibration analysis of elastically restrained ends FGM beams with porosities[J]. Aerospace Science and Technology, 2014, 32(1): 111-120. doi: 10.1016/j.ast.2013.12.002 [32] SHAFIEI N, MIRJAVADI S S, RABBY B, et al. Vibration of two-dimensional imperfect functionally graded (2D-FG) porous nano-/micro-beams[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 322: 615-632. doi: 10.1016/j.cma.2017.05.007 [33] ZHANG B, HE M, LIU D, et al. Size-dependent functionally graded beam model based on an improved third-order shear deformation theory[J]. European Journal of Mechanics A: Solids, 2014, 47: 211-230. doi: 10.1016/j.euromechsol.2014.04.009 [34] ŞIMŞEK M. Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories[J]. Nuclear Engineering and Design, 2010, 240(4): 697-705. doi: 10.1016/j.nucengdes.2009.12.013 [35] AKGÖZ B, CIVALEK Ö. Free vibration analysis of axially functionally graded tapered Bernoulli-Euler microbeams based on the modified couple stress theory[J]. Composite Structures, 2013, 98: 314-322. doi: 10.1016/j.compstruct.2012.11.020 -
计量
- 文章访问数: 762
- HTML全文浏览量: 404
- PDF下载量: 99
- 被引次数: 0
渝公网安备50010802005915号