Grain Boundary Slip and a Grain Boundary Triple Junction Crack Nucleation Model for Nanocrystals Under the Influence of Hydrogen
-
摘要: 在远场均匀拉伸载荷下，裂纹尖端会产生应力集中，与裂纹尖端相邻的晶界会承受较大的切应力，此切应力会导致晶界滑移. 该文研究了氢和纳米晶界滑移对晶界裂纹形核、临界应力强度因子以及屏蔽效应的影响. 应用连续分布位错方法给出了模型的理论解. 结果表明：由于位错在晶界三叉点和滑移带尖端处的塞积，楔形裂纹会优先沿着晶界三叉点DC方向和晶界BD向上萌生，而且氢会使得裂纹萌生的总能量降低，氢浓度每增加1%，萌生最稳定裂纹的总能量大约降低1.86%. 虽然晶界滑移会使得裂纹尖端的临界应力强度因子和屏蔽效应增大, 但是氢使得临界应力强度因子降低. 最后根据弱键理论，研究了氢对表面能的影响，氢浓度每增加1%，表面能降低5%. 这一理论工作提供了氢和晶界滑移对材料微观断裂力学的新信息，有助于解释金属断裂的微观机理.Abstract: Under the far-field uniform tensile load, the crack tip will generate stress concentration, and the grain boundary adjacent to the crack tip will bear large shear stresses to cause nanograin boundary slip. The effects of hydrogen and nanoboundary slip on the crack nucleation, the critical stress intensity factor and the shielding action were investigated. The theoretical solution of the model was given with the continuous distributed dislocation method. The results show that, the wedge cracks preferentially germinate along direction DC of the grain boundary triple junction and grain boundary BD due to the plugging of the dislocation at the grain boundary triple junction and the tip of the slip plane. Moreover, hydrogen decreases the total energy of crack initiation. When hydrogen concentration increases by 1%, the total energy of the most stable crack initiation will decrease by about 1.86%. Although the grain boundary slip increases the critical stress intensity factor and the shielding action at the crack tip, hydrogen will decrease the critical stress intensity factor. Finally, according to the hydrogen enhanced decohesion (HEDE) theory, the influence of hydrogen on surface energy was studied. With every 1% increase of the hydrogen concentration, the surface energy will decrease by 5%. This theoretical work provides new information on the microscopic fracture mechanics of materials caused by hydrogen and grain boundary slip, and helps to explain the microscopic mechanism of metal fracture.
-
0. 引言
纳米晶体材料由于其晶粒尺寸非常小且晶界体积分数很大，导致其与传统的粗晶材料相比而言具有独特的力学、化学和物理特性(具有较高的强度、延展性和良好的抗损耗性能等)，这使得纳米材料成为当今比较热点的一个研究领域.
目前，纳米晶体材料的主要塑性变形机制包括晶界滑移、晶粒旋转和晶界扩散等[1-2]. 以上主要的塑性变形机制不仅使得高集中应力松弛，阻碍了纳米裂纹的形核，而且还可以减缓或者阻止所形成裂纹的生长. 因此，这些变形机制可以有效地提高纳米晶体材料的断裂韧性. 这与仿真模拟结果和实验数据比较一致[3]. Ovid’ko等[4]研究了晶界滑移和晶界迁移对纳米晶体和陶瓷裂纹生长和扩展的影响. 研究结果表明，此两种协同机制可以使得纳米晶金属和陶瓷的临界应力强度因子增加数倍，因此，它可能会导致这些材料的断裂韧性显著增强，而且在以上所研究的两部分中，认为晶界滑移占据了主要作用. Wang等[1]提出了一个理论模型，研究了晶界扩散调节下的晶界滑动对变形纳米晶材料中三重结纳米孔洞形核的影响. 在高应变速率下，纳米空隙由于GB滑动而成核. 然后，他们又研究了纳米空穴在三重结处的形核过程，得到了纳米空穴的平衡半径. Jiang和Carter[5]基于第一性原理计算了金属铁和铝中存在不同量氢时的理想断裂能(表面能)，结果发现，金属的理想断裂能量几乎随着氢覆盖的增加而线性下降，在半单层氢时下降了45%，这表明当氢原子存在时，金属晶体凝聚力大幅度降低. 即氢在表面的吸附或在界面处的偏聚会削弱表面形成能和界面结合强度，导致材料的解理破坏. 采用电化学纳米压痕技术研究了电化学充氢对奥氏体不锈钢力学性能的原位影响, 位错周围的氢分布增加了位错核半径并降低了位错线能量，从而促进了位错成核[6].
在过去一段时间，晶界变形机制、主裂纹尖端位错发射和氢对材料力学性能的影响等方面的研究一直备受关注，但是对于纳米晶体材料而言，同时考虑氢影响下的晶界变形机制，裂纹尖端位错发射的研究相对甚少. 因此本文首先基于分子动力学的相关模拟，理论推导出氢的引入对材料力学参数的影响，定量给出了氢浓度对表面能、晶格摩擦力、原子键合力等力学参数的影响；其次，本文同时考虑了晶界滑移机制和裂纹尖端位错的发射，研究了裂纹尖端发射的位错列与晶界滑移之间的相互影响；进一步研究了氢对三叉点处微裂纹萌生和滑移带塞积尖端微裂纹萌生的促进作用，并且对三叉点处楔形裂纹萌生的方向做出了相应的判断；最后，分别讨论了氢和晶界滑移对临界应力强度因子的影响. 另外，将连续分布位错方法应用于求解裂纹尖端位错发射和晶界变形机制，扩展了连续分布位错方法的应用范围，为分析晶体材料微观变形机理、裂纹萌生和裂纹扩展的行为提供了理论方法上的支撑.
1. 氢影响下的晶界三叉点和晶界处裂纹形核模型
1.1 基本模型描述
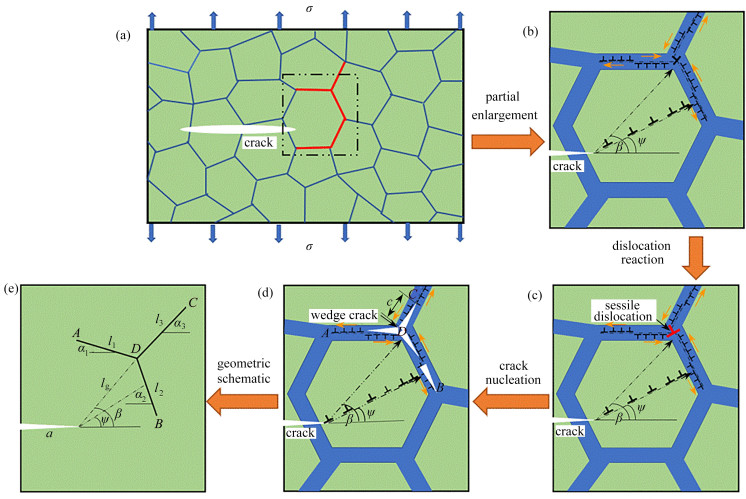
如图 1所示，纳米晶体受远场均匀拉伸载荷，材料内部预置一条半长为a的主裂纹. 图 1(a)为远场均匀拉伸载荷下晶界滑动引起楔形裂纹形核示意图；图 1(b)为晶界三叉点处晶界滑动和裂纹尖端位错发射的局部放大图；图 1(c)为晶界三叉点处发生位错反应，产生不动位错以及在滑移带尖端位错塞积；图 1(d)为晶界三叉点处位错不断反应和滑移带尖端位错塞积最终导致裂纹形核；图 1(e)为模型几何关系简图. 由于裂纹尖端的应力集中，产生滑移的晶界数目较多，而本文为了简化模型，仅考虑裂纹尖端附近一个晶界三叉点的位置. 在切应力作用下，产生晶界滑移，晶界滑移产生位错偶极子，位错偶极子在切应力作用下分别沿着晶界DA，DB和DC运动，最终在晶界三叉点处塞积引发位错反应，生成不动位错[7]. 另外，裂纹尖端的应力集中也会使得裂纹尖端作为位错源发射位错，发射的位错在切应力的作用下沿着滑移带运动，最终在滑移带尖端塞积. 位错的塞积会积累大量的应变能，材料通过裂纹扩展或萌生的方式释放应变能集中. 滑移带的长度为lg，由于裂纹尖端刚进入晶内，因此本模型中可认为是晶粒尺寸. 主裂纹与滑移面、晶界三叉点的夹角分别为ψ和β；晶界DA，DB和DC的长度分别为l1，l2和l3，夹角分别为α1，α2和α3(取逆时针方向为正).
图 1 主裂纹尖端位错发射与晶界滑移导致纳米裂纹萌生的过程示意图注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同.Figure 1. Schematic diagram of the initiation process of a nanocrack caused by dislocation emission and grain boundary slip at the main crack tip1.2 利用叠加原理求解理论模型
根据叠加原理，图 1中所描述的模型可分成两个子问题求解. 子问题1是无限大平面内无缺陷，只受均匀拉伸载荷. 子问题2可描述为一个无限大平面内含五列位错，而无外载荷的作用[8-9]. 子问题1的应力可表示为
$$ \tilde{\sigma}_{y y}(x, y)=\sigma, \tilde{\sigma}_{x y}(x, y)=0 . $$ (1) 对于子问题2的求解，由位错引起的沿位错带i的应力分量可通过坐标变换得到，另外为了描述方便，裂纹，晶界AD，BD和CD，滑移带分别记为“1”、“2”、“3”、“4”和“5”：
$$ \begin{gathered} \bar{\sigma}_{J l}^{j i}\left(\xi_j, x_i, d_{j i}, \theta_{j i}, \alpha_{j i}\right)=\frac{2 \mu}{\pi(1+\kappa)}\left[b_{x_j} G_{x j J I}^{j i}\left(\xi_j, x_i, d_{j i}, \theta_{j i}, \alpha_{j i}\right)+b_{y_j} G_{y j J I}^j\left(\xi_j, x_i, d_{j i}, \theta_{j i}, \alpha_{j i}\right)\right], \\ J I=x_i y_i, y_i y_i ; i, j=1, 2, 3, 4, 5, \end{gathered} $$ (2) 式中，μ是剪切模量；κ是Kolosovs常数，κ=3－4ν；b是Burgers向量的分量，ν是Poisson比；G(ξj, xi, dji, θji, αji)是影响函数, 用于描述晶格中位错所引起的原子位移的分布，表征了位错周围原子的畸变程度和分布情况. 影响函数可以理解为从位错的应力场中推导出来，位错是晶体中的线状缺陷，它会引起应力场的扰动，从而导致晶格中原子的位移. 影响函数可以描述这种位移随距离的变化规律，通过影响函数可以推导出位错的应力、应变、位移等. 它的第一个下标与Burgers的分量对应，后两个下标与产生的应力分量对应[10]. 另外，关于影响函数初始的表达式以及位错列之间的影响函数在文献[11]中有具体的推导. σJIji是位错带j上位错引起的沿位错带i的应力, 因此，由位错带j中的总位错引起的沿着位错带i的应力可以通过从－Rj到Rj的积分计算. 则位错列的应力分量可表示为
$$ \left\{\begin{array}{l} \bar{\sigma}_{y_j y_i}\left(x_i\right)=\frac{2 \mu}{\pi(1+\kappa)} \sum\limits_{j=1}^5 \int_{-R_j}^{R_j}\left[B_{x_j}\left(\xi_j\right) G_{x_j {y_j y_i}}^{j i}\left(\xi_j, x_i, d_{j i}, \theta_{j i}, \alpha_{j i}\right)+\right. \\ \left.\quad B_{y_j}\left(\xi_j\right) G_{y_j y_i y_i}^{j i}\left(\xi_j, x_i, d_{j i}, \theta_{j i}, \alpha_{j i}\right)\right] \mathrm{d} \xi_j, \\ \bar{\sigma}_{x_i y_i}\left(x_i\right)=\frac{2 \mu}{\pi(1+\kappa)} \sum\limits_{j=1}^5 \int_{-R_j}^{R_j}\left[B_{x_j}\left(\xi_j\right) G_{x_j x_i y_i}^{j i}\left(\xi_j, x_i, d_{j i}, \theta_{j i}, \alpha_{j i}\right)+\right. \\ \left.B_{y_j}\left(\xi_j\right) G_{y_j x_i y_i}^{j i}\left(\xi_j, x_i, d_{j i}, \theta_{j i}, \alpha_{j i}\right)\right] \mathrm{d} \xi_j, \end{array}\right. $$ (3) 式中，Rj是位错列半长.
在准静态平衡状态下，需满足以下四个条件：①裂纹面为自由表面，沿着裂纹面应力分量为零；②晶界上位错偶极子运动的切应力等于晶界上位错运动的阻力；③滑移面上位错运动的阻力等于晶格摩擦力；④裂纹面上无净位错，另外由于位错偶极子成对出现，晶界上也满足无净位错. 方程式表示如下：
$$ \tilde{\sigma}_{y y}+\bar{\sigma}_{y y}=0, \tilde{\sigma}_{x y}+\bar{\sigma}_{x y}=0, $$ (4) $$ \left\{\begin{array}{l} \tilde{\sigma}_{y y} \sin \alpha_1 \cos \alpha_1+\bar{\sigma}_{x_2 y_2}\left(x_2\right)=\tau_0, \\ \tilde{\sigma}_{y y} \sin \alpha_2 \cos \alpha_2+\bar{\sigma}_{x_3 y_3}\left(x_3\right)=\tau_0, \\ \tilde{\sigma}_{y y} \sin \alpha_3 \cos \alpha_3+\bar{\sigma}_{x_4 y_4}\left(x_4\right)=\tau_0, \end{array}\right. $$ (5) $$ \widetilde{\sigma}_{y y} \sin \psi \cos \psi+\bar{\sigma}_{x_5 y_5}\left(x_5\right)=\tau_{\mathrm{f}}, $$ (6) $$ \left\{\begin{array}{l} \int_{-a}^a B_{x_1}\left(\xi_1\right) \mathrm{d} \xi_1=\int_{-a}^a B_{y_1}\left(\xi_1\right) \mathrm{d} \xi_1=0, \\ \int_{-0.5 l_1}^{0.5 l_1} B_{x_2}\left(\xi_2\right) \mathrm{d} \xi_2=\int_{-0.5 l_2}^{0.5 l_2} B_{x_3}\left(\xi_3\right) \mathrm{d} \xi_3=\int_{-0.5 l_3}^{0.5 l_3} B_{x_4}\left(\xi_4\right) \mathrm{d} \xi_4=0, \end{array}\right. $$ (7) 式中，τ0是晶界位错运动的阻力，τf是晶格摩擦力，B是位错密度函数. 位错密度函数表示为$ B(s)= w(s) \phi(s), \phi(s)$是未知函数，对晶界和裂纹$ w(s)=\frac{1}{\sqrt{1-s^2}}$，对滑移带$ w(s)=\frac{\sqrt{1-s}}{\sqrt{1+s}}$ [8]. 由于方程式(4)—(7)的数值解很难得到，因此利用Gauss-Chebyshev积分方法离散化处理，离散后可得如下结果：
$$ \left\{\begin{array}{l} \frac{2 \mu}{\pi(1+\kappa)} \sum\limits_{j=1}^5 \frac{R_j}{n} \sum\limits_{I=1}^n\left[\phi_{x_j}\left(s_I\right) G_{x_j y_i y_i}^{i j}\left(s_I, t_K, d_{j i}, \theta_{j i}, \alpha_{j i}\right)+\right. \\ \left.\quad \phi_{y_j}\left(s_I\right) G_{y_j y_i y_i}^{j i}\left(s_I, t_K, d_{j i}, \theta_{j i}, \alpha_{j i}\right)\right]+\sigma=0, \\ \frac{2 \mu}{\pi(1+\kappa)} \sum\limits_{j=1}^5 \frac{R_j}{n} \sum\limits_{I=1}^n\left[\phi_{x_j}\left(s_I\right) G_{x_j x_i y_i}^{j i}\left(s_I, t_K, d_{j i}, \theta_{j i}, \alpha_{j i}\right)+\right. \\ \left.\quad \phi_{y_j}\left(s_I\right) G_{y_j x_i y_i}^{j i}\left(s_I, t_K, d_{j i}, \theta_{j i}, \alpha_{j i}\right)\right]+\sigma=0, \end{array}\right. $$ (8) (9) (10) $$ \sum\limits_{I=1}^n \phi_{x_1}\left(s_I\right)=\sum\limits_{I=1}^n \phi_{y_1}\left(s_I\right)=\sum\limits_{I=1}^n \phi_{x_2}\left(s_I\right)=\sum\limits_{I=1}^n \phi_{x_3}\left(s_I\right)=\sum\limits_{I=1}^n \phi_{x_4}\left(s_I\right)=0 \text {, } $$ (11) 式中，sI是积分点，tK是配置点，表达式为
$$ \left\{\begin{array}{l} s_I=\cos \frac{\pi(2 I-1)}{2 n}, \quad I=1, 2, 3, \cdots, n, \\ t_K=\cos \frac{\pi K}{n}, \quad K=1, 2, 3, \cdots, n-1 . \end{array}\right. $$ (12) 由于晶界上的位错平行于晶界，即为滑移位错，可建立如下方程：
$$ \phi_{y_2}\left(s_I\right)=\phi_{y_3}\left(s_I\right)=\phi_{y_4}\left(s_I\right)=0 . $$ (13) 结合式(8)—(11) 和式(13)，解得未知函数ϕ(sI). 代入B(s)=w(s)ϕ(s)，得沿着晶界和滑移带的位错密度函数. 滑移带上的位错数目沿着滑移带对位错密度函数积分，即$ n=\int_{-0.5 l_{\mathrm{g}}}^{0.5 l_{\mathrm{g}}} B_{x_5}\left(\xi_5\right) \mathrm{d} \xi_5$，而沿着晶界上的位错偶极子数目可通过下式积分得到：
$$ N_{A D}=\int_{x_{20}}^{0.5 l_1} B_{x_2}\left(\xi_2\right) \mathrm{d} \xi_2, N_{B D}=\int_{x_{30}}^{0.5 l_2} B_{x_3}\left(\xi_3\right) \mathrm{d} \xi_3, N_{C D}=\int_{x_{40}}^{0.5 l_3} B_{x_4}\left(\xi_4\right) \mathrm{d} \xi_4, $$ (14) 式中，NDA，NDB和NDC分别是晶界DA，DB和DC上的位错偶极子数；x20，x30和x40分别是位错密度函数为零的点.
位错偶极子在切应力的驱动下运动到晶界三叉点处，发生位错反应，合成不动位错的Burgers矢量为
$$ \left\{\begin{array}{l} b_x=b\left(N_{D B} \cos \alpha_2+N_{D A} \cos \alpha_1-N_{D C} \cos \alpha_3\right), \\ b_y=b\left(N_{D B} \sin \alpha_2-N_{D A} \sin \alpha_1-N_{D C} \sin \alpha_3\right), \end{array}\right. $$ (15) 式中，bx和by是不动位错Burgers矢量的分量. 不动位错确定后，此模型演化为无限大平面内含一条裂纹、一条滑移带和一个不动位错的问题，应力场的计算同上述计算过程一样，此处不再赘述. 接下来可计算晶界、晶内和晶界三叉点处楔形裂纹萌生、位错发射的屏蔽效应和临界应力强度因子.
2. 结果分析
2.1 氢对材料表面能的影响
由于金属材料中存在缺陷且相比于金属原子氢原子非常小，导致氢原子很容易渗入金属材料和吸附在材料表面，从而影响材料的力学性能[12]. 在材料疲劳断裂过程中，氢的渗入和吸附会加速材料破环，其机理可能是氢改变了材料的微观结构，使材料性能发生变化. 当氢吸附在金属表面时，会使得该表面的表面能由γ降为γ(H)，并且根据Griffith相关理论，材料的断裂韧性正比于$ \sqrt{\gamma}$，因此当表面能降低时，断裂韧性也随之降低. Zhou等[13]应用MD模拟得到当原子比为C(H)=1%时，氢使原子键合力降低了5%，并且当C(H)=0.1时，原子键合力降低了50%.
剪切模量与原子键合力之间的关系如下[14]：
$$ \sigma_{\text {th }}=\frac{2 \mu(1+\nu) a_0}{\pi d} \text {, } $$ (16) 式中，σth是原子键合力，a0是原子平衡间距，d是平面距离. 假设氢仅影响原子键合力，对ν，a0和d没有影响[12-13]. 基于式(16)可得到
$$ \mu(\mathrm{H}) / \mu=\sigma_{\mathrm{th}}(\mathrm{H}) / \sigma_{\mathrm{th}} \text {. } $$ (17) 原子键合力与表面能的关系如下[12]：
$$ \sigma_{\mathrm{th}}=\left[\frac{2 \mu(1+\nu) \gamma}{a_0}\right]^{1 / 2}, $$ (18) 式中，γ是表面能. 基于式(17)和(18)可得
$$ \sigma_{\mathrm{th}}(\mathrm{H}) / \sigma_{\mathrm{th}}=\gamma(\mathrm{H}) / \gamma \text {. } $$ (19) Wang等[15]基于第一性原理对铁铝合金的原子键合力和表面能进行了分析，计算结果表明：氢原子使得原子键合力下降与氢使得表面能下降的幅度一致，故可近似认为表面能与原子键合力成正比例关系.
2.2 晶界上位错偶极子数目与外加载荷的关系
本文以面心立方纳米晶体铝为研究对象，材料参数[16-17]如下：γ=1.2 J · m－2, γb=0.5 J · m－2, b=0.286 nm, ν=0.34, μ=27 GPa, τf=34.4 MPa, τ0=20 MPa，其中，γb是晶界开裂能量. 由于纯铝为FCC晶体，则选取(111)为滑移面. 在很多实验中观察到，材料的断裂面位于(001)晶面上[18]，因此本文考虑裂纹面位于(001)的情况. 根据晶面夹角公式计算得夹角为50°左右，即取ψ=50°.
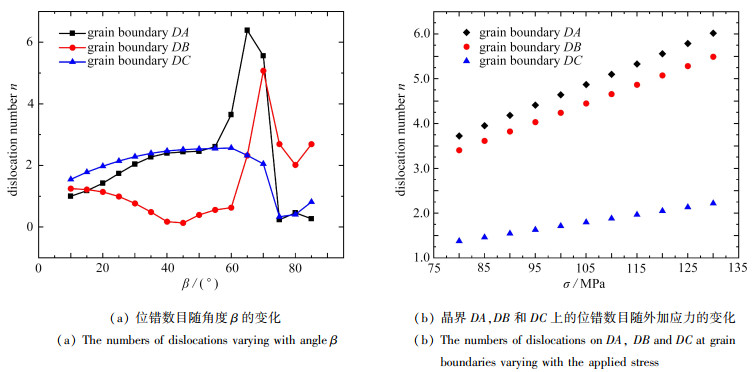
图 2给出了位错数目随角度β和外加应力的变化，所取得计算参数为a=5 000 nm, lg=70 nm, α1=－15°, α2=60°, α3=－65°, ψ=50°, β=70°, l1=l2=l3=70 nm. 由图 2(a)可知，β会影响三叉点处晶界DA，DB和DC上位错偶极子的数量，进而由式(15)可知会影响位错反应后形成的不动位错的Burgers矢量，从图中可发现在β=70°左右时，形成超位错的Burgers矢量较大，因此说明晶体在该角度下易形成超位错，以及在外力作用下位错比较容易运动. 因此本文在后续计算中选取了β=70°. 如图 2(b)所示，三个晶界的长度都取70 nm, 通过计算出每个晶界上位错偶极子的数量可以发现，随着外加应力的增大，三个晶界上产生位错偶极子的数量也在增加.虽然每个晶界的长度相同，但是三个晶界上产生位错偶极子的数量完全不同而且差距较大. 晶界DA上的数量最多，晶界DB次之，晶界DC上数量最少. 产生以上结果的原因可能是晶界DA平面最接近最大剪切平面，所受到的剪切应力最大，晶界滑移最严重，导致相应晶界上产生位错偶极子的数量增加.
图 2 位错数目随角度β和外加应力的变化Figure 2. The numbers of dislocations varying with angle β and the applied stress2.3 位错发射对裂纹尖端应力强度因子屏蔽效应的影响
为了计算发射位错对裂纹尖端应力强度因子的屏蔽效应，引入屏蔽效应参数δ，定义如下：
$$ \delta=1-\frac{K_{\mathrm{I}}}{K_{\mathrm{a}}}, $$ (20) 式中，Ka是由外加载荷贡献的应力强度因子，KⅠ是由施加载荷和发射位错产生的裂纹尖端处的局部应力强度因子. 由于发射位错对裂纹尖端的屏蔽效应，KⅠ一般小于Ka，因此0 < δ < 1，而且δ越大，表明位错发射对裂纹扩展的屏蔽效应越大. Ka和KⅠ的表达式如下：
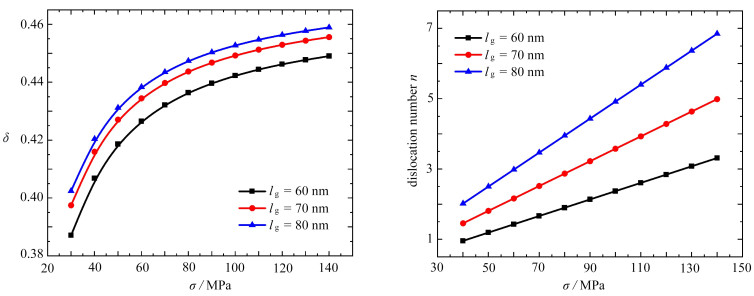
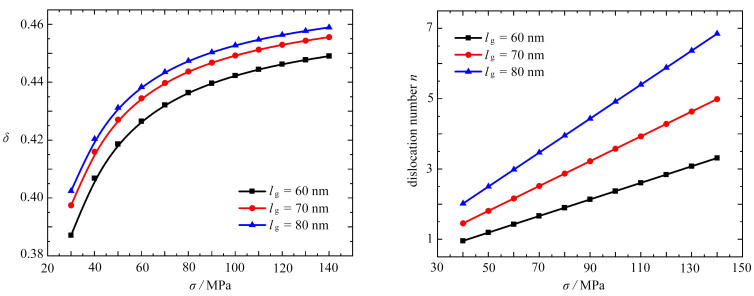
$$ K_{\mathrm{a}}=\sigma \sqrt{\pi a}, K_{\mathrm{I}}=\frac{2 \mu}{1+\kappa} \sqrt{\pi a} \phi_y(+1) . $$ (21) 屏蔽效应δ和裂纹尖端发射位错数n随外加载荷σ的变化曲线如图 3所示，首先，从图中可以看出随着外加载荷的增大，δ呈非线性增加，滑移带上的位错数目n呈线性增加. 对裂纹扩展的屏蔽效应是由发射位错产生的背应力产生的，因此发射位错的数量越多，屏蔽效应越大，使得裂纹尖端钝化越严重. 另外从图中可以看出随着晶粒尺寸的增加，裂纹尖端发射的位错数目和屏蔽效应也都增大，这是因为晶粒尺寸越大，所能容纳的位错数目越多，则对裂纹尖端的钝化效果越显著. 因此增加晶粒尺寸在一定程度上可以改善材料的断裂韧性[19].
图 3 裂纹尖端屏蔽效应和位错发射数目随外加载荷的变化关系Figure 3. Relationships between the emission numbers of crack tip dislocations and shielding effects with applied loads2.4 晶界滑移和氢对晶界三叉点和晶界楔形裂纹萌生的影响
如图 1所示，假设萌生楔形裂纹的长度为c, 根据断裂力学理论，裂纹萌生的总能量可以用单位裂纹长度的表面能和能量释放率表示[20]：
$$ \frac{\partial E_{\mathrm{c}}}{\partial c}=2 \gamma_{\mathrm{e}}-G=2 \gamma_{\mathrm{e}}-\left[\frac{1-\nu^2}{E}\left(k_{\mathrm{I}}^2+k_{\mathrm{II}}^2\right)\right], $$ (22) 式中，E是弹性模量，kⅠ，kⅡ为Ⅰ型和Ⅱ型应力强度因子. 另外，当楔形裂纹在晶内萌生或扩展时，γe=γ，而在晶界上萌生或扩展时，γe=γ－0.5γb. 对于楔形裂纹，裂纹尖端应力强度因子的表达式为[21]
$$ k_{\mathrm{I}}=\sigma_{\mathrm{n}} \sqrt{\frac{\pi c}{2}}+\frac{E W_{\mathrm{n}}}{4\left(1-\nu^2\right)} \sqrt{\frac{2}{\pi c}}, $$ (23) $$ k_{\text {II }}=\sigma_{\mathrm{t}} \sqrt{\frac{\pi c}{2}}+\frac{E W_{\mathrm{t}}}{4\left(1-\nu^2\right)} \sqrt{\frac{2}{\pi c}}, $$ (24) 式中，σn和σt分别是远场应力施加在裂纹上的法向和切向的应力分量；Wn和Wt表示裂纹法向和切向的楔形强度分量，如下所示：
$$ \left\{\begin{array}{l} W_{\mathrm{n}}=N_{A D} b \sin \varphi_1+N_{B D} b \sin \varphi_2+N_{C D} b \sin \varphi_3, \\ W_{\mathrm{t}}=N_{A D} b \cos \varphi_1+N_{B D} b \cos \varphi_2+N_{C D} b \cos \varphi_3, \end{array}\right. $$ (25) 式中，φ1，φ2和φ3表示裂纹萌生方向与位错滑移方向之间的夹角.
另外为了判断楔形裂纹的萌生，还需要分别计算晶界三叉点处和滑移带尖端位错塞积的总能量Es, 其表达式如下[21]：
$$ E_{\mathrm{s}}=\frac{N_{A D} D b^2}{2} \ln \frac{l_{\mathrm{g}}}{r_0}+\frac{N_{B D} D b^2}{2} \ln \frac{l_{\mathrm{g}}}{r_0}+\frac{N_{C D} D b^2}{2} \ln \frac{l_{\mathrm{g}}}{r_0}, $$ (26) 式中，r0为位错芯半径，一般取r0=2b，$ D=\frac{\mu}{2 \pi(1-\nu)}$.
通过以上计算，已经得到了位错塞积群的总能量以及楔形裂纹萌生的总能量. 然后通过比较这两个能量的大小来判断楔形裂纹是否能萌生，位错塞积引起的总能量和楔形裂纹萌生的总能量之差为
$$ \Delta E=E_{\mathrm{s}}-E_{\mathrm{c}} \cdot $$ (27) 若ΔE>0，可以产生楔形裂纹，反之则不产生楔形裂纹.
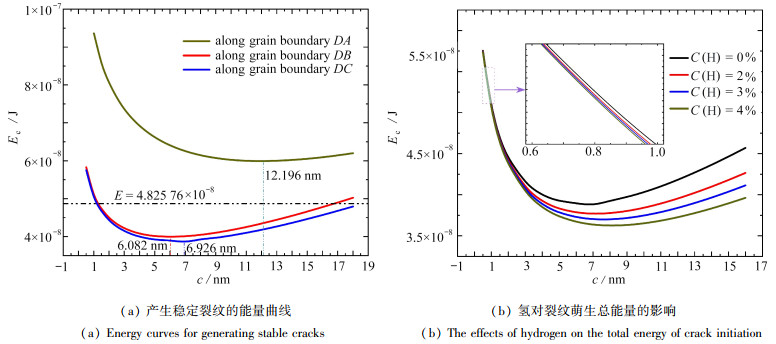
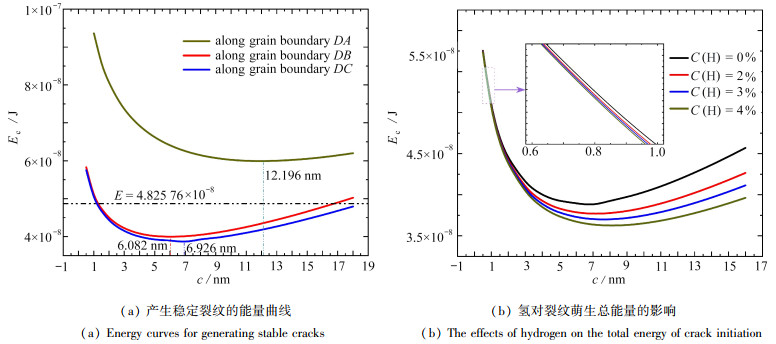
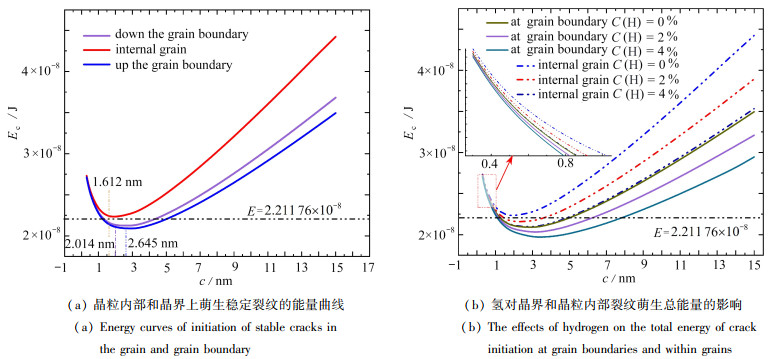
图 4为沿不同晶界的裂纹萌生总能量和氢对裂纹萌生总能量的影响，所取计算参数为σ=120 MPa, lg=70 nm. 如图 4(a)所示，计算了晶界三叉点处楔形裂纹萌生的总能量，曲线的最低点，即$ \partial E_{\mathrm{c}} / \partial c=0$的解为平衡裂纹的长度，并且在虚线以下(即ΔE>0)能量越低，萌生的裂纹越稳定，而在虚线以上(即ΔE < 0)，不会萌生微裂纹. 从图中可以看出，在晶界三叉点处萌生最稳定的裂纹长度为6.082 nm和6.926 nm, 分别计算了沿着晶界DA，DB和DC萌生稳定楔形裂纹的能量，对应的最低能量分别为5.962 5×10－8 J，3.987 4×10－8 J和3.846 3×10－8 J. 由计算结果可知沿着晶界DC的方向最容易萌生楔形裂纹，因为沿着晶界DC萌生裂纹所需的能量较低. 图 4(b)选取图 4(a)中最容易萌生楔形裂纹的晶界DC，计算了不同氢浓度对裂纹萌生总能量的影响. 从图中看出随着氢浓度的增大，楔形裂纹萌生所需的总能量逐渐降低，并且氢浓度每增加1%，萌生最稳定楔形裂纹的总能量大概降低了1.86%. 但是从局部放大图中可以看出，氢浓度的改变对萌生较短楔形裂纹总能量的影响微乎其微. 产生以上结果的主要原因是氢的渗入使材料的表面能和晶界开裂的能量降低. 由于位错在晶界三叉点和滑移带尖端的塞积，导致局部应力集中严重，而材料为了释放局部应力集中通常以裂纹萌生或者扩展方式，裂纹扩展和萌生时需形成上下两个新表面，即需要的能量为2γe.
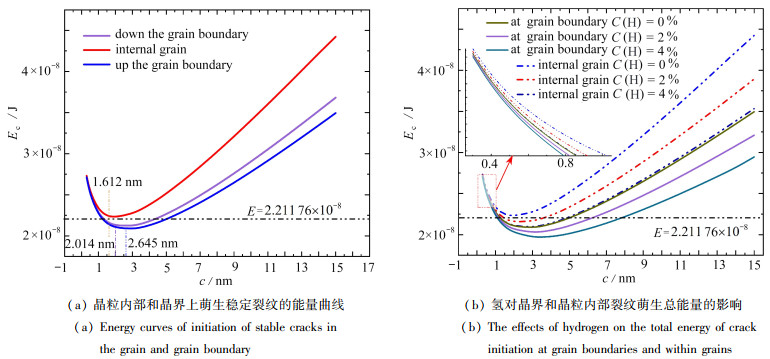
图 4 沿不同晶界的裂纹萌生总能量和氢对裂纹萌生总能量的影响Figure 4. The total energy of crack initiation along different grain boundaries and the effects of hydrogen on the total energy of crack initiation裂纹尖端发射的位错沿着滑移带运动，最终在滑移带尖端塞积，位错的塞积容易导致裂纹萌生. 楔形裂纹萌生可能发生在位错塞积部分的晶粒或最靠近塞积的晶界处. 因此会存在一个先后关系. 计算结果如图 5(a)所示，晶粒内部萌生长度为1.612 nm的楔形裂纹所需的总能量为2.216 4×10－8 J，在沿晶界DB向下产生2.014 nm的楔形裂纹所需的能量为2.118 6×10－8 J，而在沿晶界DB向上产生2.645 nm的楔形裂纹所需的能量为2.076 5×10－8 J. 晶界处产生稳定平衡裂纹的能量与在晶粒内部产生稳定平衡裂纹的能量相比，晶界上产生的裂纹长度更长，释放的能量更少. 因此，相比较晶粒内部，晶界处楔形裂纹的萌生更加容易，而且沿着晶界DB向上最有利于楔形裂纹萌生. 而且从图中可以发现晶粒内部楔形裂纹萌生所需的总能量曲线在虚线以上，这表明在此计算模型下晶粒内部不会产生楔形裂纹. 图 5(b)选取图 5(a)中沿晶界DB向上和晶粒内部裂纹萌生总能量的值，讨论氢浓度对萌生楔形裂纹总能量的影响. 从图中可以看出随着氢浓度的增大，晶界上和晶粒内部裂纹萌生的总能量都降低，而且在此计算模型下，无氢时晶粒内部本身不能萌生微裂纹，如图中蓝色虚线所示，但是随着氢的引入，导致蓝色虚线开始下降，最终在一定的氢浓度下也可以萌生楔形裂纹. 因此氢促进了晶内和晶界上楔形裂纹的萌生.
图 5 不同位置处裂纹萌生的总能量和氢对裂纹萌生总能量的影响Figure 5. The total energy of crack initiation at different locations and the effects of hydrogen on the total energy of crack initiation2.5 晶界滑移和氢对临界应力强度因子的影响
根据线弹性断裂力学的相关理论，裂纹扩展过程中释放的应变能等于形成新裂纹面所需的能量，因此满足如下关系式[22]：
$$ \varphi_{\mathrm{n}}=G_{\mathrm{Ic}}=\left\{\begin{array}{l} 2 \gamma, \\ 2 \gamma-\gamma_{\mathrm{b}}, \end{array}\right. $$ (28) 式中，φn是内聚能，GⅠc是能量释放率. 在不同方向上，裂纹尖端能量释放率不同，任意方向上能量释放率与应力强度因子的表达式如下[23]：
$$ G_{\mathrm{Ic}}=\frac{1-\nu}{2 \mu}\left[k_{\mathrm{I}}^{\prime}(\delta)^2+k_{\mathrm{II}}^{\prime}(\delta)^2\right], $$ (29) 式中
$$ \left\{\begin{array}{l} k_{\mathrm{I}}^{\prime}(\delta)=\frac{1}{2} \cos (\delta / 2)\left[K_{\mathrm{I}}(1+\cos \delta)-3 K_{\text {II }} \sin \delta\right], \\ k_{\text {II }}^{\prime}(\delta)=\frac{1}{2} \cos (\delta / 2)\left[K_{\mathrm{I}} \sin \delta+K_{\text {II }}(3 \cos \delta-1)\right], \end{array}\right. $$ (30) δ为裂纹尖端极坐标的任意方向，$ K_{\text {II }}=\frac{2 \mu}{1+\kappa} \sqrt{\pi a} \phi_x(+1)$.
根据Griffith脆性断裂理论，解理断裂的临界应力强度因子可通过下式计算得到：
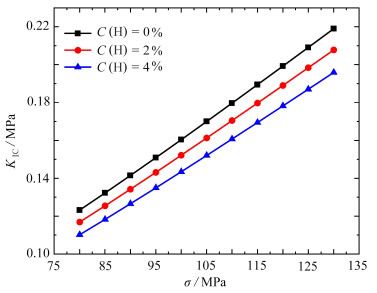
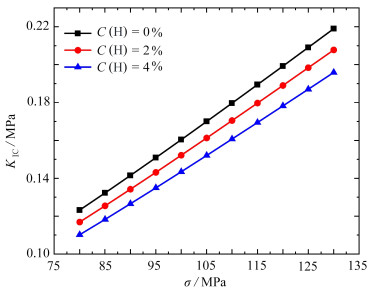
$$ K_{\mathrm{Ic}}=\sqrt{\frac{E \varphi_{\mathrm{n}}}{1-\nu^2}} . $$ (31) 如图 6所示，首先计算了无氢时晶界滑移对临界应力强度因子的影响，如图中黑线所示，结果表明：随着外加载荷的增大，晶界滑动的强度越大，临界应力强度因子也逐渐增大. 这一计算结果说明，晶界滑动提高了位错发射的临界应力强度因子，导致刃型位错越难从裂纹尖端发射出来. 同时，由于晶界滑动可能发生从裂纹尖端到晶界位错源的转变[24]. 另外从式(28)可以发现，裂纹尖端的能量释放率与表面能相关，氢的引入会使得材料的表面能降低，因此计算了不同氢浓度对临界应力强度因子的影响. 从图中可以发现随着氢浓度的增加，临界应力强度因子等幅度的减小. 综上可述，晶界滑移对临界应力强度因子起正作用，而氢起负作用.
图 6 临界应力强度因子随外加载荷的变化Figure 6. Changes of the critical stress intensity factor with the applied load3. 结论
本文基于连续分布位错方法，主要分析了氢影响下纳米晶体主裂纹尖端附近楔形裂纹的形核机理，通过能量判据对楔形裂纹的萌生长度给出了理论解. 对于纳米晶体材料，考虑由于晶界滑动导致位错在晶界三叉点处塞积和裂纹尖端位错发射在滑移带尖端的塞积引发的楔形裂纹形核，同时分析了氢促进裂纹形核和使位错发射临界应力强度因子下降的原因. 主要结论如下：
1) 在晶界三叉点处沿着晶界DC最容易萌生稳定的楔形裂纹，滑移带尖端的位错塞积最容易沿着晶界DB向上萌生楔形裂纹.
2) 氢的引入降低了裂纹萌生的总能量，氢浓度每增加1%，萌生最稳定裂纹的总能量大概降低1.86%. 表明氢可以促进裂纹尖端附近楔形裂纹的形核.
3) 晶界滑动强度越大，裂纹尖端位错发射的临界应力强度因子越大，另外随着氢浓度的增加，临界应力强度因子等幅度的减小.
4) 通过弱键理论，推导出氢对材料表面能的影响，即氢浓度每增加1%，表面能降低5%. 一定程度上可说明氢降低键合力和氢降低表面能理论是一致的.
-
图 1 主裂纹尖端位错发射与晶界滑移导致纳米裂纹萌生的过程示意图
注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同.
Figure 1. Schematic diagram of the initiation process of a nanocrack caused by dislocation emission and grain boundary slip at the main crack tip
图 2 位错数目随角度β和外加应力的变化
Figure 2. The numbers of dislocations varying with angle β and the applied stress
图 3 裂纹尖端屏蔽效应和位错发射数目随外加载荷的变化关系
Figure 3. Relationships between the emission numbers of crack tip dislocations and shielding effects with applied loads
图 4 沿不同晶界的裂纹萌生总能量和氢对裂纹萌生总能量的影响
Figure 4. The total energy of crack initiation along different grain boundaries and the effects of hydrogen on the total energy of crack initiation
图 5 不同位置处裂纹萌生的总能量和氢对裂纹萌生总能量的影响
Figure 5. The total energy of crack initiation at different locations and the effects of hydrogen on the total energy of crack initiation
-
[1] WANG L, ZHOU J, ZHANG S, et al. Effects of accommodated grain boundary sliding on triple junction nanovoid nucleation in nanocrystalline materials[J]. Mechanics of Materials, 2014, 71 (4): 10-20. [2] FENG H, FANG Q H, ZHANG L C, et al. Special rotational deformation and grain size effect on fracture toughness of nanocrystalline materials[J]. International Journal of Plasticity, 2013, 42 (4): 50-64. [3] MEIROM R A, CLARK T E, MUHLSTEIN C L. The role of specimen thickness in the fracture toughness and fatigue crack growth resistance of nanocrystalline platinum films[J]. Acta Materialia, 2012, 60 (3): 1408-1417. doi: 10.1016/j.actamat.2011.11.015 [4] OVID'KO I A, SHEINERMAN A G, AIFANTIS E C. Effect of cooperative grain boundary sliding and migration on crack growth in nanocrystalline solids[J]. Acta Materialia, 2011, 59 (12): 5023-5031. doi: 10.1016/j.actamat.2011.04.056 [5] JIANG D E, CARTER E A. First principles assessment of ideal fracture energies of materials with mobile impurities: implications for hydrogen embrittlement of metals[J]. Acta Materialia, 2004, 52 (16): 4801-4807. doi: 10.1016/j.actamat.2004.06.037 [6] BARNOUSH A, ASGARI M, JOHNSEN R. Resolving the hydrogen effect on dislocation nucleation and mobility by electrochemical nanoindentation[J]. Scripta Materialia, 2012, 66 (6): 414-417. doi: 10.1016/j.scriptamat.2011.12.004 [7] OVID'KO I A. Review on the fracture processes in nanocrystalline materials[J]. Journal of Materials Science, 2007, 42 (5): 1694-1708. doi: 10.1007/s10853-006-0968-9 [8] HILLS D A, KELLY P A, DAI D N, et al. Solution of Crack Problems: the Distributed Dislocation Technique[M]. Netherlands: Kluwer Academic Publishers, 2013. [9] 孙奇, 吴金波, 江晓禹. 次表面分岔裂纹的力学行为[J]. 应用数学和力学, 2023, 44 (12): 1453-1462. doi: 10.21656/1000-0887.440056SUN Qi, WU Jinbo, JIANG Xiaoyu. Mechanical behavior of subsurface branched cracks[J]. Applied Mathematics and Mechanics, 2023, 44 (12): 1453-1462. (in Chinese) doi: 10.21656/1000-0887.440056 [10] 邢帅兵, 王强胜, 生月, 等. 圆形杂质对裂纹扩展的影响[J]. 应用数学和力学, 2019, 40 (2): 189-199. doi: 10.21656/1000-0887.390136 XING Shuaibing, WANG Qiangsheng, SHENG Yue, et al. Effects of circular inhomogeneity on crack propagation[J]. Applied Mathematics and Mechanics, 2019, 40 (2): 189-199. (in Chinese) doi: 10.21656/1000-0887.390136 [11] LI X, JIANG X, LI X, et al. Solution of an inclined crack in a finite plane and a new criterion to predict fatigue crack propagation[J]. International Journal of Mechanical Sciences, 2016, 119 : 217-223. doi: 10.1016/j.ijmecsci.2016.10.019 [12] ZHANG J, SHENG Y, YANG H, et al. Crystal crack dislocation model and microcrack nucleation criterion in the hydrogen environment[J]. European Journal of Mechanics A: Solids, 2023, 98 : 104899. doi: 10.1016/j.euromechsol.2022.104899 [13] ZHOU G H, ZHOU F X, WAN F R, et al. Molecular dynamics simulation of hydrogen enhancing dislocation emission[J]. Science in China Series E: Technological Sciences, 1998, 145/149 : 123-128. [14] CHEREPANOV G P. Mechanics of brittle fracture[J]. Journal of Applied Mechanics, 1982, 49 (4): 932. [15] WANG F, WANG C. First-principles investigation of hydrogen embrittlement in polycrystalline Ni3Al[J]. Physical Review B, 1998, 57 (1): 289-295. doi: 10.1103/PhysRevB.57.289 [16] OVID'KO I A, SHEINERMAN A G, AIFANTIS E C. Stress-driven migration of grain boundaries and fracture processes in nanocrystalline ceramics and metals[J]. Acta Materialia, 2008, 56 (12): 2718-2727. doi: 10.1016/j.actamat.2008.02.004 [17] LI X J X. Revealing the inhibition mechanism of grain size gradient on crack growth in gradient nano-grained materials[J]. International Journal of Solids and Structures, 2019, 172/173 : 1-9. doi: 10.1016/j.ijsolstr.2019.05.023 [18] SABNIS P A, MAZIERE M, FOREST S, et al. Effect of secondary orientation on notch-tip plasticity in superalloy single crystals[J]. International Journal of Plasticity, 2012, 28 (1): 102-123. [19] LI X, SHEINERMAN A G, YANG H, et al. Theoretical modeling of toughening mechanisms in the CrMnFeCoNi high-entropy alloy at room temperature[J]. International Journal of Plasticity, 2022, 154 : 103304. [20] ZHANG F, LIU Y, ZHOU J. The crack nucleation in hierarchically nanotwinned metals[J]. Engineering Fracture Mechanics, 2018, 201 : 29-35. [21] WU M S, ZHOU H. An energy analysis of triple junction crack nucleation due to the wedging action of grain boundary dislocations[J]. International Journal of Fracture, 1996, 78 (2): 165-191. [22] GIBSON M A, SCHUH C A. Segregation-induced changes in grain boundary cohesion and embrittlement in binary alloys[J]. Acta Materialia, 2015, 95 : 145-155. [23] NUISMER R J. An energy release rate criterion for mixed mode fracture[J]. International journal of fracture, 1975, 11 (2): 245-250. [24] SHIMOKAWA T, TANAKA M, KINOSHITA K, et al. Roles of grain boundaries in improving fracture toughness of ultrafine-grained metals[J]. Physical Review B, 2011, 83 (21): 214113. -
下载:
下载:
计量
- 文章访问数: 1117
- HTML全文浏览量: 163
- PDF下载量: 23
- 被引次数: 0
渝公网安备50010802005915号