基于改进正余弦算法的抱杆结构优化

杨小猛; 李亮; 胡雄飞; 周焕林

doi:10.21656/1000-0887.440354

基于改进正余弦算法的抱杆结构优化

doi: 10.21656/1000-0887.440354

1.
合肥工业大学土木与水利工程学院，合肥 230009
2.
国网安徽省电力有限公司建设分公司，合肥 230071
3.
国网安徽省电力有限公司安庆供电公司，安徽安庆 246001

(我刊编委周焕林来稿)

基金项目:

国家自然科学基金 11972143

详细信息

作者简介:
杨小猛(1995—)，男，硕士(E-mail: Yxiaomeng123@outlook.com)

通讯作者:
周焕林(1973—)，男，教授，博士，博士生导师(通讯作者. E-mail: zhouhl@hfut.edu.cn)

中图分类号: TU318
计量
- 文章访问数: 205
- HTML全文浏览量: 86
- PDF下载量: 51
- 被引次数: 0
出版历程
- 收稿日期: 2023-12-14
- 修回日期: 2024-01-23
- 刊出日期: 2024-05-01

Structure Optimization of Holding Poles Based on the Improved Sine Cosine Algorithm

1.
College of Civil Engineering, Hefei University of Technology, Hefei 230009, P.R.China
2.
State Grid Anhui Electric Power Co., Ltd. Construction Branch, Hefei 230071, P.R.China
3.
State Grid Anhui Electric Power Co., Ltd. Anqing Electric Power Supply Company, Anqing, Anhui 246001, P.R.China

(Contributed by ZHOU Huanlin, M. AMM Editorial Board)

摘要

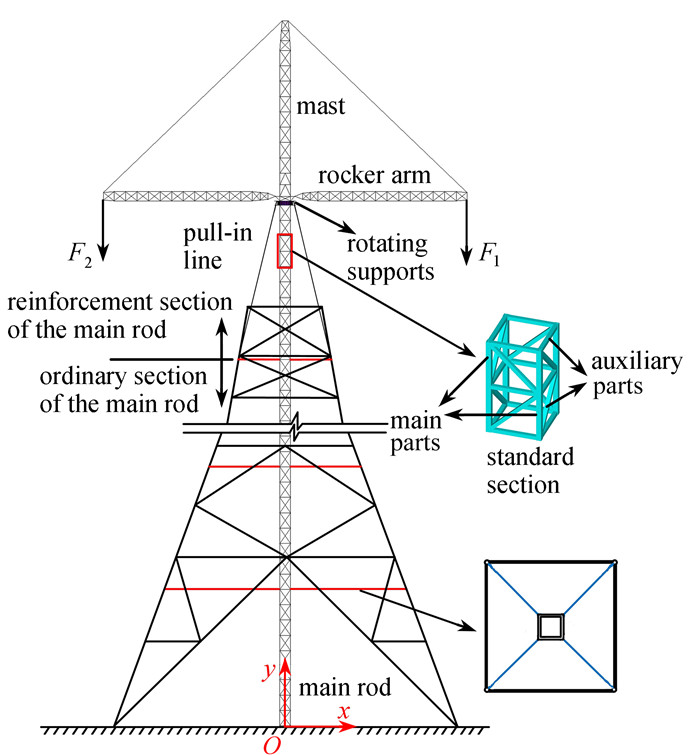
摘要: 抱杆是组立输电铁塔的特种起重设备. 以最小质量为优化目标，杆件的截面尺寸、辅材连接方式以及摇臂节点坐标为优化变量，许用应力、位移和屈曲系数为约束条件，建立抱杆优化设计模型. 提出一种改进的正余弦算法(improved sine cosine algorithm，ISCA)，开展抱杆尺寸、形状和拓扑优化. 引入Lévy飞行增强算法全局搜索能力，采用精英引导策略增强算法局部搜索能力，使用贪婪选择策略更新最优解. 算例表明ISCA能够有效求解空间桁架结构的优化设计问题.
- 正余弦算法 /
- 抱杆 /
- 桁架结构 /
- 结构优化 /
- 有限元分析
Abstract: The holding pole is a special lifting device for the construction of transmission towers. The optimization design model for the holding pole was established. The minimum mass was set as the optimization objective. The cross-section sizes of members, the connection modes of auxiliary members and the coordinates of the rocker joint were set as the optimization variables. The allowable stress, displacement and buckling coefficient were taken as the constraining conditions. An improved sine cosine algorithm (ISCA) was proposed to carry out the size, shape and topology optimization designs of the holding pole. For the ISCA, the Lévy flight was introduced to enhance the global search ability, elite guidance strategy was applied to enhance the local search ability, and the greedy selection strategy was used to update the optimal solution. The example shows that, the ISCA can effectively solve the optimization design problems of spatial truss structures.
- sine cosine algorithm /
- holding pole /
- truss structure /
- structure optimization /
- finite element analysis
edited-by

edited-by
注释:

1) (我刊编委周焕林来稿)

HTML全文

图 1 抱杆整体示意图

Figure 1. Overall diagram of the holding pole

下载: 全尺寸图片幻灯片

图 2 摇臂方位和风载荷方向

Figure 2. Rocker arm orientations and wind load directions

下载: 全尺寸图片幻灯片

图 3 ISCA优化流程图

Figure 3. The ISCA optimization flowchart

下载: 全尺寸图片幻灯片

图 4 摇臂节点移动模型

Figure 4. The rocker arm node movement model

下载: 全尺寸图片幻灯片

图 5 标准节排布形式

Figure 5. The standard section arrangement

下载: 全尺寸图片幻灯片

图 6 优化收敛曲线

Figure 6. Optimization convergence curves

下载: 全尺寸图片幻灯片

图 7 应力对比

Figure 7. Stress comparison

下载: 全尺寸图片幻灯片

图 8 最大顶端位移对比

Figure 8. Comparison of maximum displacements

下载: 全尺寸图片幻灯片

图 9 屈曲系数对比

Figure 9. Comparison of buckling coefficients

下载: 全尺寸图片幻灯片

表 1 抱杆各段角钢型号

Table 1. The angle steel model for each part of the holding pole

	main part	auxiliary part
ordinary	∟80×6	∟63×5
reinforcement	∟90×8	∟63×5
mast	∟90×8	∟60×6
rocker	∟65×6	∟50×6
mass	13.64 t

下载: 导出CSV

表 2 载荷工况

Table 2. Load cases

load case		lifted weight	wind direction	rocker orientation
max unbalance loading	case 1	4 t, 3 t	0°	45°
	case 2	4 t, 3 t	45°	45°
	case 3	4 t, 3 t	90°	45°
high wind	case 4	-	0°	45°
	case 5	-	45°	45°
	case 6	-	90°	45°

下载: 导出CSV

表 3 各工况分析结果

Table 3. Analysis results of each working condition

load case		max Mises stress σ_m/MPa		top displacement u_t/mm	buckling coefficient
load case		main part	auxiliary part	top displacement u_t/mm	buckling coefficient
working	case 1	166.53	76.47	259.82	4.01
	case 2	169.19	84.48	268.47	3.93
	case 3	168.41	75.15	248.93	4.00
high wind	case 4	173.19	58.42	243.36	3.80
	case 5	181.43	47.94	252.56	3.62
	case 6	180.58	44.54	244.19	3.57

下载: 导出CSV

表 4 优化结果

Table 4. Optimization results

algorithm	A₁	A₂	A₃	A₄	A₅	A₆	A₇	A₈	y₁	y₅	T₁	T₂	T₃	T₄	mass W/t
ISCA	∟70×6	∟45×3	∟80×7	∟45×3	∟75×7	∟45×3	∟45×5	∟45×4	80	-150	5	3	4	2	10.44
SCA	∟70×6	∟45×3	∟90×8	∟45×4	∟75×8	∟50×6	∟50×6	∟50×5	90	-50	2	1	3	1	11.18

下载: 导出CSV

参考文献(18)

[1]	陶然, 周焕林, 孟增, 等. 基于响应面法和改进算术优化算法的抱杆优化设计[J]. 应用数学和力学, 2022, 43(10): 1113-1122. doi: 10.21656/1000-0887.420318 TAO Ran, ZHOU Huanlin, MENG Zeng, et al. Optimization design of holding pole based on response surface methodology and improved arithmetic optimization algorithm[J]. Applied Mathematics and Mechanics, 2022, 43(10): 1113-1122. (in Chinese) doi: 10.21656/1000-0887.420318
[2]	方林, 蒋晓琳, 周庆丰, 等. 基于改进天鹰优化器的抱杆结构优化[J]. 科学技术与工程, 2023, 23(27): 11759-11767. doi: 10.12404/j.issn.1671-1815.2023.23.27.11759 FANG Lin, JIANG Xiaolin, ZHOU Qingfeng, et al. Structure optimization of holding pole based on improved aquila optimizer[J]. Science Technology and Engineering, 2023, 23(27): 11759-11767. (in Chinese) doi: 10.12404/j.issn.1671-1815.2023.23.27.11759
[3]	刘宸宇, 骆烜赫, 刘康翔, 等. 基于平铺刚度法的弧形加筋板的轻量化设计[J]. 应用数学和力学, 2023, 44(8): 953-964. doi: 10.21656/1000-0887.430342 LIU Chenyu, LUO Xuanhe, LIU Kangxiang, et al. Light weight design of arc rib stiffened plate based on the smeared stiffener method[J]. Applied Mathematics and Mechanics, 2023, 44(8): 953-964. (in Chinese) doi: 10.21656/1000-0887.430342
[4]	杜晨, 彭雄奇. 变厚度连续纤维增强复合材料铺层设计优化方法[J]. 应用数学和力学, 2022, 43(12): 1313-1323. doi: 10.21656/1000-0887.420410 DU Chen, PENG Xiongqi. Lamination design optimization for continuous fiber reinforced composites of variable thicknesses[J]. Applied Mathematics and Mechanics, 2022, 43(12): 1313-1323. (in Chinese) doi: 10.21656/1000-0887.420410
[5]	郭惠勇, 宋小辉, 李正良. 基于改进人工鱼群算法的输电塔塔腿拓扑优化[J]. 振动与冲击, 2017, 36(4): 52-58. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201704009.htm GUO Huiyong, SONG Xiaohui, LI Zhengliang. Topology optimization of transmission tower legs based on an improved artificial fish-swarm algorithm[J]. Journal of Vibration and Shock, 2017, 36(4): 52-58. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201704009.htm
[6]	石开荣, 潘文智, 姜正荣, 等. 基于生长空间限定与并行搜索的模拟植物生长算法的空间结构优化方法[J]. 建筑结构学报, 2021, 42(7): 85-94. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB202107010.htm SHI Kairong, PAN Wenzhi, JIANG Zhengrong, et al. Optimization method of spatial structures based on growth space limited & parallel search-based plant growth simulation algorithm[J]. Journal of Building Structures, 2021, 42(7): 85-94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB202107010.htm
[7]	SOUZA R R D, MIGUEL L F F, LOPEZ R H, et al. A procedure for the size, shape and topology optimization of transmission line tower structures[J]. Engineering Structures, 2016, 111: 162-184. doi: 10.1016/j.engstruct.2015.12.005
[8]	KHODZHAIEV M, REUTER U. Structural optimization of transmission towers using a novel genetic algorithm approach with a variable length genome[J]. Engineering Structures, 2021, 240: 112306. doi: 10.1016/j.engstruct.2021.112306
[9]	FIORE A, MARANO G C, GRECO R, et al. Structural optimization of hollow-section steel trusses by differential evolution algorithm[J]. International Journal of Steel Structures, 2016, 16(2): 411-423. doi: 10.1007/s13296-016-6013-1
[10]	RENKAVIESKI C, PARPINELLI R S. Meta-heuristic algorithms to truss optimization: literature mapping and application[J]. Expert Systems With Applications, 2021, 182: 115197. doi: 10.1016/j.eswa.2021.115197
[11]	MIRJALILI S. SCA: a sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96: 120-133. doi: 10.1016/j.knosys.2015.12.022
[12]	ATTIA A F, EL SEHIEMY R A, HASANIEN H M. Optimal power flow solution in power systems using a novelsine-cosine algorithm[J]. International Journal of Electrical Power & Energy Systems, 2018, 99: 331-343.
[13]	EWEES A A, ELAZIZ M A, AL-QANESS M A A, et al. Improved artificial bee colony using sine-cosine algorithm for multi-level thresholding image segmentation[J]. IEEE Access, 2020, 8: 26304-26315. doi: 10.1109/ACCESS.2020.2971249
[14]	ABUALIGAH L, DULAIMI A J. A novel feature selection method for data mining tasks using hybrid sine cosine algorithm and genetic algorithm[J]. Cluster Computing, 2021, 24(3): 2161-2176. doi: 10.1007/s10586-021-03254-y
[15]	ABDEL-MAWGOUD H, FATHY A, KAMEL S. An effective hybrid approach based on arithmetic optimization algorithm and sine cosine algorithm for integrating battery energy storage system into distribution networks[J]. Journal of Energy Storage, 2022, 49: 104154. doi: 10.1016/j.est.2022.104154
[16]	LI N, WANG L. Bare-bones based sine cosine algorithm for global optimization[J]. Journal of Computational Science, 2020, 47: 101219. doi: 10.1016/j.jocs.2020.101219
[17]	LONG W, WU T, LIANG X, et al. Solving high-dimensional global optimization problems using an improved sine cosine algorithm[J]. Expert Systems With Applications, 2019, 123: 108-126. doi: 10.1016/j.eswa.2018.11.032
[18]	GANDOMI A H, YANG X S, ALAVI A H. Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems[J]. Engineering With Computers, 2013, 29(1): 17-35. doi: 10.1007/s00366-011-0241-y